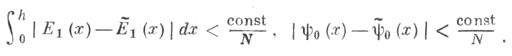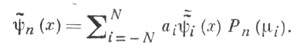|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СФЕРИЧЕСКИХ ГАРМОНИК МЕТОДЗначение СФЕРИЧЕСКИХ ГАРМОНИК МЕТОД в математической энциклопедии: способ приближенного решения кинетич. уравнения с помощью разложения фазовой плотности частиц в конечную сумму по сферич. функциям от аргументов, задающих направление скорости частицы (см. [1]). Метод широко применяется при решении задач нейтронной физики.
Система вида
возникает при условии
Для уравнения (1) типичные краевые условия имеют вид:
Таковы, напр., краевые условия для задачи нейтронной физики о критич. режиме слоя толщины hсо свободными поверхностями х=0 и x=h (границы с вакуумом). В этой задаче необходимо найти положительное решение (1), (6) и собственное значение с. ВС. г. м. вместо (6) естественно взять
Однако такой подход дает в два раза больше условий, чем необходимо для частного решения системы (3). На практике был испытан различный выбор значений пв (7). Наилучший результат дают условия с n=2k+1, k=0, 1, .... N-1. Для односкоростного уравнения переноса общего вида из Владимирова вариационного принципа получается система уравнений С. г. м. и указанные граничные условия (при выборе пробных функций в виде линейной комбинации сферических гармоник). Для трехмерной геометрии граничные условия можно записать в виде
Здесь r- вектор пространственной координаты,
Система С. г. м. (3) при граничных условиях, аналогичных (6),
Приближенное собственное значение сходится к точному со скоростью 1/N2.
Метод дискретных ординат в одномерной геометрии эквивалентен С. г. м. (см. [3]), т. к. система (10) может быть получена из (3) спомощью линейного преобразования неизвестных функций:
Однако в многомерных задачах С. г. м. в низших приближениях дает большую точность, чем метод дискретных ординат. Лит.:[1] Mapчук Г. И., Лебедев В. И., Численные методы в теории переноса нейтронов, 2 изд., М., 1981; [2] Султангазин У. М., лЖ. вычисл. матем. и матем. физ.
|
|
|
|

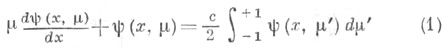
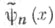 - приближенных значений коэффициентов Фурье
- приближенных значений коэффициентов Фурье 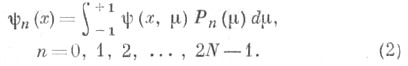
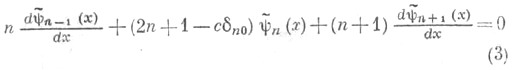
 Здесь
Здесь  - фазовая плотность частиц, распространяющихся в веществе, с - среднее число вторичных частиц, возникающих в одном акте взаимодействия с частицами вещества,
- фазовая плотность частиц, распространяющихся в веществе, с - среднее число вторичных частиц, возникающих в одном акте взаимодействия с частицами вещества, 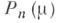 - многочлен Лежандра степени п. Система (3) определяет Р 2N-1 -приближение С. г . м. для уравнения (1). Приближенное значение фазовой плотности
- многочлен Лежандра степени п. Система (3) определяет Р 2N-1 -приближение С. г . м. для уравнения (1). Приближенное значение фазовой плотности 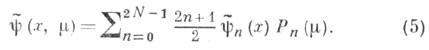
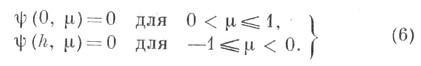
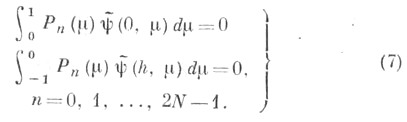

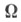 - единичный вектор скорости частицы, имеющий сферич. координаты
- единичный вектор скорости частицы, имеющий сферич. координаты  - единичный вектор внешней нормали к кусочно гладкой поверхности Г, ограничивающей выпуклую область пространства, в к-рой решается задача
- единичный вектор внешней нормали к кусочно гладкой поверхности Г, ограничивающей выпуклую область пространства, в к-рой решается задача 
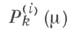 - присоединенные функции Лежандра 1-го рода
- присоединенные функции Лежандра 1-го рода  - многочлены Лежандра).
- многочлены Лежандра).  (см. [2]). Скорость сходимости
(см. [2]). Скорость сходимости 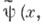
 легко оценить, сравнив интегральные уравнения для
легко оценить, сравнив интегральные уравнения для 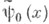 и
и  т. е. оценив близость их ядер. Уравнение (1) с граничными условиями (6) приводит к интегральному уравнению с ядром
т. е. оценив близость их ядер. Уравнение (1) с граничными условиями (6) приводит к интегральному уравнению с ядром 
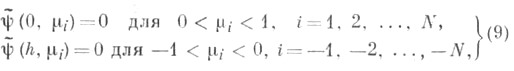
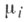 - корни
- корни 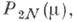 приводит к интегральному уравнению с ядром
приводит к интегральному уравнению с ядром 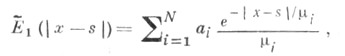
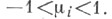 Особенность, к-рую имеет функция
Особенность, к-рую имеет функция 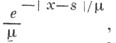 приводит к медленной сходимости при больших N:
приводит к медленной сходимости при больших N: