СФЕРИЧЕСКАЯ ГАРМОНИКА

Значение СФЕРИЧЕСКАЯ ГАРМОНИКА в математической энциклопедии:

степени k - сужение однородного гармонического многочлена h^(k) (х)степени kот ппеременных х= (х ₁..... х _n )на единичной сфере S^n-1 евклидова пространства Е ^п, Bчастности, при п=3 С. г. - это классич. сферические функции.

Пусть Основным свойством С. г. является свойство ортогональности: если и - С. г. соответственно степеней kи l, причем то

Простейшими С. г. являются зональные сферические гармоники. Для любого и любого k>0 существует зональная С. г. постоянная на любой параллели сферы S^n-1,ортогональной вектору t'. Зональные С. г. лишь постоянным множителем отличаются от Лежандра многочленов при п=3 или от ультрасферических многочленов при n>3:

где многочлены определяются при через производящую функцию

Многочлены k= 0, 1, . . ., ортогональны свесом и образуют ортогональный базис пространства Если f( х') - функция из пространства L²(Sⁿ-1), причем то существует единственный набор С. г. Y^(k) такой, что

причем ряд сходится по норме L²(Sⁿ-1).
Разложения по С. г. во многом аналогичны разложениям в ряды Фурье, обобщением к-рых они в сущности являются. Однородные гармонические многочлены h^(k) (х)иногда наз. пространственными С. г. В силу однородности

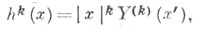
в связи с чем С. г. иногда наз. также поверхностными С. г.

Лит.:[1] Морс Ф. М., Фешбах Г., Методы теоретической физики, пер. с англ., т. 1-2, М., 1960; [2] Стейн И., Вейс Г., Введение в гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974.
Е. Д. Соломенцев.