"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СУЩЕСТВЕННО ОСОБАЯ ТОЧКА
Значение СУЩЕСТВЕННО ОСОБАЯ ТОЧКА в математической энциклопедии:
изолированная особая точка а однозначного характера аналитич. ции f(z) комплексного переменного z, для к-рой не существует никакого, конечного или бесконечного, предела 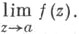 В достаточно малой проколотой окрестности
В достаточно малой проколотой окрестности  С. о. т.
С. о. т.  или
или 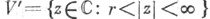 в случае
в случае  функция f(z)разлагается в ряд Лорана
функция f(z)разлагается в ряд Лорана

или соответственно

причем в главной части этих рядов имеется бесконечно много отличных от нуля коэффициентов с k с отрицательными индексами k.
Сохоцкого теорема показывает, что любое комплексное значение wиз расширенной комплексной плоскости  является предельным для функции f(z) в любой сколь угодно малой окрестности С. о. т. а. Согласно Пикара теореме, любое конечное комплексное значение
является предельным для функции f(z) в любой сколь угодно малой окрестности С. о. т. а. Согласно Пикара теореме, любое конечное комплексное значение  за исключением, быть может, одного, даже принимается функцией f(z), и притом бесконечно часто, в любой окрестности С. о. т. а. Теорему Сохоцкого иначе выражают, говоря, что предельное множество С (а; f) функции f(z) в С. о. т. а совпадает со всей расширенной плоскостью
за исключением, быть может, одного, даже принимается функцией f(z), и притом бесконечно часто, в любой окрестности С. о. т. а. Теорему Сохоцкого иначе выражают, говоря, что предельное множество С (а; f) функции f(z) в С. о. т. а совпадает со всей расширенной плоскостью  Для регулярных точек и полюсов это множество, напротив, вырожденное, т. е. сводится к одной точке
Для регулярных точек и полюсов это множество, напротив, вырожденное, т. е. сводится к одной точке  Поэтому в более общем смысле существенно особой точкой аналитпч. функции f(z) наз. всякая такая особая точка а(не обязательно изолированная), в к-рой не существует конечного или бесконечного предела
Поэтому в более общем смысле существенно особой точкой аналитпч. функции f(z) наз. всякая такая особая точка а(не обязательно изолированная), в к-рой не существует конечного или бесконечного предела  или, иначе говоря, в к-рой предельное множество С(а; f) невырожденное. Теоремы Сохоцкого и Пикара для таких С. о. т., не являющихся изолированными точками множества всех особых точек, доказаны лишь при нек-рых дополнительных предположениях. Напр., эти теоремы остаются в силе для изолированной точки амножества С. о. т., в частности для предельной точки аполюсов мероморфной функции.
или, иначе говоря, в к-рой предельное множество С(а; f) невырожденное. Теоремы Сохоцкого и Пикара для таких С. о. т., не являющихся изолированными точками множества всех особых точек, доказаны лишь при нек-рых дополнительных предположениях. Напр., эти теоремы остаются в силе для изолированной точки амножества С. о. т., в частности для предельной точки аполюсов мероморфной функции.
Точка а= (а 1, . . ., а n )комплексного пространства  наз. точкой мероморфности аналитич. ции f(z) многих комплексных переменных z=(zl, ... , zn), если f(z) есть мероморфная функция в нек-рой окрестности Uточки а, т. е. если f(z) пред-ставима в Uв виде отношения двух голоморфных функций f(z)=p(z)/q(z),
наз. точкой мероморфности аналитич. ции f(z) многих комплексных переменных z=(zl, ... , zn), если f(z) есть мероморфная функция в нек-рой окрестности Uточки а, т. е. если f(z) пред-ставима в Uв виде отношения двух голоморфных функций f(z)=p(z)/q(z), Существенно особыми точками аналитич. ции f(z) многих комплексных переменных наз. особые точки афункции f(z), не являющиеся точками мероморфности. При этом невырожденность предельного множества . (а; f) перестает быть характеристическим свойством С. о. т.
Существенно особыми точками аналитич. ции f(z) многих комплексных переменных наз. особые точки афункции f(z), не являющиеся точками мероморфности. При этом невырожденность предельного множества . (а; f) перестает быть характеристическим свойством С. о. т.
Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2]Фукс Б. А., Введение в теорию аналитич. ций многих комплексных переменных, М., 1962.
Е. Д. Соломенцев.

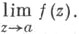 В достаточно малой проколотой окрестности
В достаточно малой проколотой окрестности  С. о. т.
С. о. т.  или
или 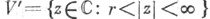 в случае
в случае  функция f(z)разлагается в ряд Лорана
функция f(z)разлагается в ряд Лорана 

 является предельным для функции f(z) в любой сколь угодно малой окрестности С. о. т. а. Согласно Пикара теореме, любое конечное комплексное значение
является предельным для функции f(z) в любой сколь угодно малой окрестности С. о. т. а. Согласно Пикара теореме, любое конечное комплексное значение  за исключением, быть может, одного, даже принимается функцией f(z), и притом бесконечно часто, в любой окрестности С. о. т. а. Теорему Сохоцкого иначе выражают, говоря, что предельное множество С (а; f) функции f(z) в С. о. т. а совпадает со всей расширенной плоскостью
за исключением, быть может, одного, даже принимается функцией f(z), и притом бесконечно часто, в любой окрестности С. о. т. а. Теорему Сохоцкого иначе выражают, говоря, что предельное множество С (а; f) функции f(z) в С. о. т. а совпадает со всей расширенной плоскостью  Для регулярных точек и полюсов это множество, напротив, вырожденное, т. е. сводится к одной точке
Для регулярных точек и полюсов это множество, напротив, вырожденное, т. е. сводится к одной точке  Поэтому в более общем смысле существенно особой точкой аналитпч. функции f(z) наз. всякая такая особая точка а(не обязательно изолированная), в к-рой не существует конечного или бесконечного предела
Поэтому в более общем смысле существенно особой точкой аналитпч. функции f(z) наз. всякая такая особая точка а(не обязательно изолированная), в к-рой не существует конечного или бесконечного предела  или, иначе говоря, в к-рой предельное множество С(а; f) невырожденное. Теоремы Сохоцкого и Пикара для таких С. о. т., не являющихся изолированными точками множества всех особых точек, доказаны лишь при нек-рых дополнительных предположениях. Напр., эти теоремы остаются в силе для изолированной точки амножества С. о. т., в частности для предельной точки аполюсов мероморфной функции.
или, иначе говоря, в к-рой предельное множество С(а; f) невырожденное. Теоремы Сохоцкого и Пикара для таких С. о. т., не являющихся изолированными точками множества всех особых точек, доказаны лишь при нек-рых дополнительных предположениях. Напр., эти теоремы остаются в силе для изолированной точки амножества С. о. т., в частности для предельной точки аполюсов мероморфной функции.  наз. точкой мероморфности аналитич. ции f(z) многих комплексных переменных z=(zl, ... , zn), если f(z) есть мероморфная функция в нек-рой окрестности Uточки а, т. е. если f(z) пред-ставима в Uв виде отношения двух голоморфных функций f(z)=p(z)/q(z),
наз. точкой мероморфности аналитич. ции f(z) многих комплексных переменных z=(zl, ... , zn), если f(z) есть мероморфная функция в нек-рой окрестности Uточки а, т. е. если f(z) пред-ставима в Uв виде отношения двух голоморфных функций f(z)=p(z)/q(z), Существенно особыми точками аналитич. ции f(z) многих комплексных переменных наз. особые точки афункции f(z), не являющиеся точками мероморфности. При этом невырожденность предельного множества . (а; f) перестает быть характеристическим свойством С. о. т.
Существенно особыми точками аналитич. ции f(z) многих комплексных переменных наз. особые точки афункции f(z), не являющиеся точками мероморфности. При этом невырожденность предельного множества . (а; f) перестает быть характеристическим свойством С. о. т.