"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СУММИРОВАНИЕ РЯДОВ ФУРЬЕ
Значение СУММИРОВАНИЕ РЯДОВ ФУРЬЕ в математической энциклопедии:
построение средних рядов Фурье с помощью суммирования методов. Наиболее развита теория С. р. Ф. по тригонометрич. системе. В этом случае для функций 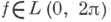 с рядами Фурье
с рядами Фурье
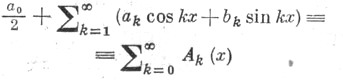
изучаются свойства средних, соответствующих рассматриваемому методу суммирования. Напр., для Абеля - Пуассона метода суммирования средними являются гармонические в единичном круге функции

а для средних арифметических метода суммирования - суммы Фейера
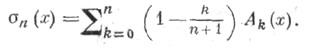
Кроме названных, наиболее важными в теории одномерных тригонометрич. рядов являются Чезаро методы суммирования, Рисса метод суммирования, Римана метод суммирования, Бернштейна - Рогозинского, метод суммирования, Балле Пуссена метод суммирования. Рассматриваются также методы суммирования, порождаемые более или менее произвольной последовательностью  -множителей
-множителей
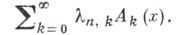
С. р. Ф. применяется в следующих задачах.
Представление функций с помощью рядов Фурье. Напр., средние Абеля - Пуассона f(r, x )при  и суммы Фейера
и суммы Фейера 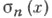 при
при  сходятся к функции f(х)в точках ее непрерывности, причем сходятся равномерно, если f непрерывна во веех точках; для каждой функции
сходятся к функции f(х)в точках ее непрерывности, причем сходятся равномерно, если f непрерывна во веех точках; для каждой функции  эти средние сходятся к ней в метрике L. Частные суммы рядов Фурье указанными свойствами не обладают.
эти средние сходятся к ней в метрике L. Частные суммы рядов Фурье указанными свойствами не обладают.
Построение полиномов с хорошими аппроксимативными свойствами. Фактически с помощью С. р. Ф. было установлено Джексона неравенство. Для решения этой задачи, наряду с использованием известных методов суммирования, были предложены новые методы - Джексона сингулярный интеграл, Балле Пуссена суммы.
В терминах средних рядов Фурье можно характеризовать многие свойства функций. Напр., функция f является существенно ограниченной в том и только том случае, когда существует такая постоянная М, что  для всех n и х.
для всех n и х.
Существенную роль играет С. р. Ф. в теории кратных тригонометрич. рядов. Так, вместо сферических частных сумм чаще используют их средние Рисса достаточно высокого порядка.
Рассматривается также С. р. Ф. по другим ортонормированным системам функций - как по конкретным системам или классам систем, напр., по ортогональным многочленам, так и по произвольным ортонормированным системам.
Лит.:[1] Бари Н. К., Тригонометрические ряды, М., 1961; [2] Зигмунд А., Тригонометрические ряды, т. 1-2, пер. с англ., М., 1965; [3] Харди Г., Расходящиеся ряды, пер. с англ., М., 1951; [4] Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с. нем., М., 1958; [5] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960.
С. А. Теляковский.

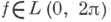 с рядами Фурье
с рядами Фурье 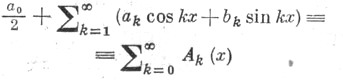

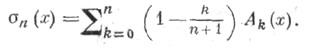
 -множителей
-множителей 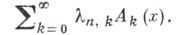
 и суммы Фейера
и суммы Фейера 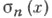 при
при  сходятся к функции f(х)в точках ее непрерывности, причем сходятся равномерно, если f непрерывна во веех точках; для каждой функции
сходятся к функции f(х)в точках ее непрерывности, причем сходятся равномерно, если f непрерывна во веех точках; для каждой функции  эти средние сходятся к ней в метрике L. Частные суммы рядов Фурье указанными свойствами не обладают.
эти средние сходятся к ней в метрике L. Частные суммы рядов Фурье указанными свойствами не обладают.  для всех n и х.
для всех n и х.