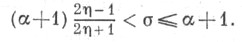"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СУММАТОРНАЯ ФУНКЦИЯ
Значение СУММАТОРНАЯ ФУНКЦИЯ в математической энциклопедии:
функции f - функция  обозначающая сумму значений f(n) на множестве натуральных чисел
обозначающая сумму значений f(n) на множестве натуральных чисел  С. ф. являются одним из основных средств выражения разнообразных свойств числовых последовательностей. Примеры С. ф.: число простых чисел
С. ф. являются одним из основных средств выражения разнообразных свойств числовых последовательностей. Примеры С. ф.: число простых чисел 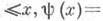
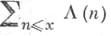 - Чебышева функция, число делителей всех
- Чебышева функция, число делителей всех 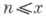 и т. п. (см. [1], [2]).
и т. п. (см. [1], [2]).
Основная задача состоит в том, чтобы найти возможно более точное асимптотич. выражение С. ф., а для С. ф., не имеющей асимптотики, наилучшую оценку ее модуля для больших значений х.
В основе аналитич. методов изучения С. ф. лежат Коши интегральная теорема и Дирихле ряды вида

Если такой ряд абсолютно сходится при 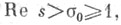 то для нецелого
то для нецелого  справедливо тождество
справедливо тождество

из к-рого, имея аналитич. родолжение F(s)переносом Пути интегрирования влево на нек-рое Re  за счет оценок интеграла по новому контуру, получается соответствующая оценка для С. ф. f. В случае
за счет оценок интеграла по новому контуру, получается соответствующая оценка для С. ф. f. В случае 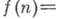
 напр., интегрирование можно перенести на
напр., интегрирование можно перенести на 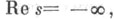 что дает формулу Римана - Мангольдтa для
что дает формулу Римана - Мангольдтa для  Из общих применений метода известна следующая теорема.
Из общих применений метода известна следующая теорема.
Предположения: f(п), l п - комплексные числа,  - действительные числа,
- действительные числа,  - положительные числа,
- положительные числа, 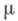 и v - целые числа
и v - целые числа 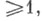 Г - гамма-функция,
Г - гамма-функция, 
1) Для любого 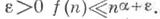
2) Определенная для 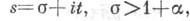 функция
функция 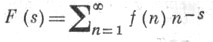 мероморфна во всей плоскости и имеет конечное число полюсов в полосе
мероморфна во всей плоскости и имеет конечное число полюсов в полосе 
3) Ряд 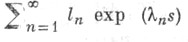 абсолютно сходится при
абсолютно сходится при 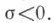
4) Для 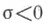
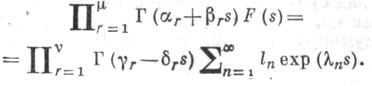
5)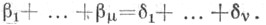
6) Если положить
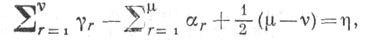 то
то 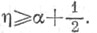
Для фиксированной полосы  найдется постоянная
найдется постоянная  такая, что
такая, что  и больших |t| имеет место оценка
и больших |t| имеет место оценка 
Заключение. Для любого 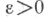 имеют
имеют
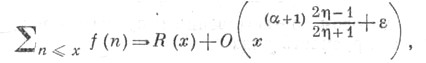
где R(х) - сумма вычетов функции 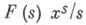 для всех ее полюсов в полосе
для всех ее полюсов в полосе
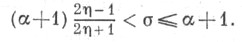
Лит.:[1] Титчмарш Е. К., Теория дзета-функции Римана, пер. с англ., М., 1953; [2] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964.
А. Ф. Лаврик.

 обозначающая сумму значений f(n) на множестве натуральных чисел
обозначающая сумму значений f(n) на множестве натуральных чисел  С. ф. являются одним из основных средств выражения разнообразных свойств числовых последовательностей. Примеры С. ф.: число простых чисел
С. ф. являются одним из основных средств выражения разнообразных свойств числовых последовательностей. Примеры С. ф.: число простых чисел 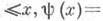
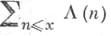 - Чебышева функция, число делителей всех
- Чебышева функция, число делителей всех 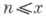 и т. п. (см. [1], [2]).
и т. п. (см. [1], [2]). 
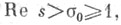 то для нецелого
то для нецелого  справедливо тождество
справедливо тождество 
 за счет оценок интеграла по новому контуру, получается соответствующая оценка для С. ф. f. В случае
за счет оценок интеграла по новому контуру, получается соответствующая оценка для С. ф. f. В случае 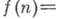
 напр., интегрирование можно перенести на
напр., интегрирование можно перенести на 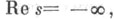 что дает формулу Римана - Мангольдтa для
что дает формулу Римана - Мангольдтa для  Из общих применений метода известна следующая теорема.
Из общих применений метода известна следующая теорема.  - действительные числа,
- действительные числа,  - положительные числа,
- положительные числа, 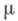 и v - целые числа
и v - целые числа 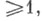 Г - гамма-функция,
Г - гамма-функция, 
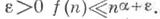
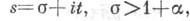 функция
функция 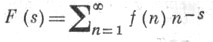 мероморфна во всей плоскости и имеет конечное число полюсов в полосе
мероморфна во всей плоскости и имеет конечное число полюсов в полосе 
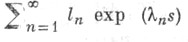 абсолютно сходится при
абсолютно сходится при 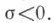
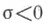
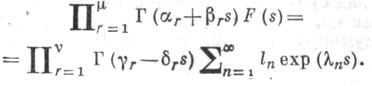
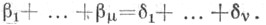
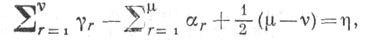 то
то 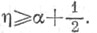
 найдется постоянная
найдется постоянная  такая, что
такая, что  и больших |t| имеет место оценка
и больших |t| имеет место оценка 
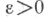 имеют
имеют 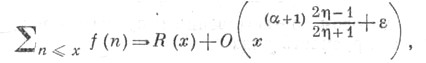
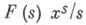 для всех ее полюсов в полосе
для всех ее полюсов в полосе