"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СТРУКТУРНО УПОРЯДОЧЕННАЯ ГРУППАЗначение СТРУКТУРНО УПОРЯДОЧЕННАЯ ГРУППА в математической энциклопедии:
решеточно упорядоченная группа, l- группа,- группа G, на множестве элементов к-рой задано отношение частичного порядка  обладающее свойствами: 1) G - решетка относительно обладающее свойствами: 1) G - решетка относительно 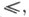 т. е. для любых т. е. для любых  существуют элементы существуют элементы 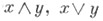 такие, что такие, что  и и  для любого для любого  выполнено выполнено  и для любого и для любого  и и  выполнено выполнено  2) для любых 2) для любых  неравенство неравенство  влечет за собой влечет за собой 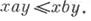 Эквивалентным образом С. у. г. может быть определена как алгебраич. система в сигнатуре Эквивалентным образом С. у. г. может быть определена как алгебраич. система в сигнатуре  удовлетворяющая аксиомам: 3) удовлетворяющая аксиомам: 3)  - группа; 4) - группа; 4) 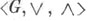 - решетка; 5) - решетка; 5)  и и  для любых для любых 
Решетка элементов С. у. г. дистрибутивна. Модулем (соответственно положительной и отрицательной частью) элемента хназ. элемент  (соответственно (соответственно 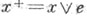 и и   В С. у. г. верны соотношения: В С. у. г. верны соотношения: 
Элементы хи у наз. ортогональными, если  Ортогональные элементы перестановочны. Подмножество H l-группы Gназ. l-подгруппой, если Н - подгруппа и подрешетка в G; l -подгруппа H наз. l- идеалом С. у. г. G, если она нормальна и выпукла в G. Множество l-подгрупп С. у. г. образует подрешетку решетки всех ее подгрупп. Решетка l-идеалов С. у. г. дистрибутивна. l - гомоморфизмом l-группы Gв l-группу H наз. гомоморфизм Ф группы Gв группу H такой, что Ортогональные элементы перестановочны. Подмножество H l-группы Gназ. l-подгруппой, если Н - подгруппа и подрешетка в G; l -подгруппа H наз. l- идеалом С. у. г. G, если она нормальна и выпукла в G. Множество l-подгрупп С. у. г. образует подрешетку решетки всех ее подгрупп. Решетка l-идеалов С. у. г. дистрибутивна. l - гомоморфизмом l-группы Gв l-группу H наз. гомоморфизм Ф группы Gв группу H такой, что 
Ядрами l-гомоморфизмов являются в точности l-идеалы l-групп. Если Gесть l-группа,  то множество то множество  для всякого для всякого  является выпуклой l-подгруппой в G. является выпуклой l-подгруппой в G.
Группа A(L)взаимно однозначных сохраняющих порядок отображений линейно упорядоченного множества L на себя есть l-группа (если для  положить положить  тогда и только тогда, когда тогда и только тогда, когда  для любого для любого  , Всякая l-группа l-изоморфна l-подгруппе С. у. г. A(L) для нек-рого подходящего множества L. , Всякая l-группа l-изоморфна l-подгруппе С. у. г. A(L) для нек-рого подходящего множества L.
Класс всех С. у. г. является многообразием сигнатуры  Важнейшее его подмногообразие- класс С. у. г., аппроксимирующихся линейно упорядоченными группами (класс представимых l -групп). Важнейшее его подмногообразие- класс С. у. г., аппроксимирующихся линейно упорядоченными группами (класс представимых l -групп).
Лит.:[1] Биркгоф Г., Теория структур, пер. с англ., М., 1952; [2] Фукс Л., Частично упорядоченные алгебраич. системы, пер. с англ., М., 1965.
В. М. Копытов.
|

 обладающее свойствами: 1) G - решетка относительно
обладающее свойствами: 1) G - решетка относительно 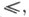 т. е. для любых
т. е. для любых  существуют элементы
существуют элементы 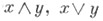 такие, что
такие, что  и
и  для любого
для любого  выполнено
выполнено  и для любого
и для любого  и
и  выполнено
выполнено  2) для любых
2) для любых  неравенство
неравенство  влечет за собой
влечет за собой 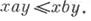 Эквивалентным образом С. у. г. может быть определена как алгебраич. система в сигнатуре
Эквивалентным образом С. у. г. может быть определена как алгебраич. система в сигнатуре  удовлетворяющая аксиомам: 3)
удовлетворяющая аксиомам: 3)  - группа; 4)
- группа; 4) 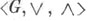 - решетка; 5)
- решетка; 5)  и
и  для любых
для любых 
 (соответственно
(соответственно 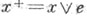 и
и 
 В С. у. г. верны соотношения:
В С. у. г. верны соотношения: 
 Ортогональные элементы перестановочны. Подмножество H l-группы Gназ. l-подгруппой, если Н - подгруппа и подрешетка в G; l -подгруппа H наз. l- идеалом С. у. г. G, если она нормальна и выпукла в G. Множество l-подгрупп С. у. г. образует подрешетку решетки всех ее подгрупп. Решетка l-идеалов С. у. г. дистрибутивна. l - гомоморфизмом l-группы Gв l-группу H наз. гомоморфизм Ф группы Gв группу H такой, что
Ортогональные элементы перестановочны. Подмножество H l-группы Gназ. l-подгруппой, если Н - подгруппа и подрешетка в G; l -подгруппа H наз. l- идеалом С. у. г. G, если она нормальна и выпукла в G. Множество l-подгрупп С. у. г. образует подрешетку решетки всех ее подгрупп. Решетка l-идеалов С. у. г. дистрибутивна. l - гомоморфизмом l-группы Gв l-группу H наз. гомоморфизм Ф группы Gв группу H такой, что 
 то множество
то множество  для всякого
для всякого  является выпуклой l-подгруппой в G.
является выпуклой l-подгруппой в G.  положить
положить  тогда и только тогда, когда
тогда и только тогда, когда  для любого
для любого  , Всякая l-группа l-изоморфна l-подгруппе С. у. г. A(L) для нек-рого подходящего множества L.
, Всякая l-группа l-изоморфна l-подгруппе С. у. г. A(L) для нек-рого подходящего множества L.  Важнейшее его подмногообразие- класс С. у. г., аппроксимирующихся линейно упорядоченными группами (класс представимых l -групп).
Важнейшее его подмногообразие- класс С. у. г., аппроксимирующихся линейно упорядоченными группами (класс представимых l -групп).