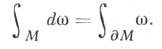|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СТОКСА ФОРМУЛАЗначение СТОКСА ФОРМУЛА в математической энциклопедии: - 1) формула, выражающая связь между потоком векторного поля через двумерное ориентированное многообразие и циркуляцию этого поля по соответствующим образом ориентированному краю этого многообразия. Пусть S - ориентированная кусочно гладкая поверхность,
(dS - элемент площади поверхности S, ds - дифференциал длины дуги края
Предложена Дж. Стоксом (G. Stokes, 1854). 2)С. ф. наз. также обобщение формулы (*), представляющее собой равенство интеграла от внешнего дифференциала дифференциальной формы
Частными случаями этой формулы являются Ньютона - Лейбница формула, Грина формула, Остроградского формула. |
|
|
|

 - единичная нормаль к поверхности S(в тех точках, конечно, где она существует), задающая ориентацию S, и пусть край поверхности Sсостоит из конечного числа кусочно гладких контуров. Через
- единичная нормаль к поверхности S(в тех точках, конечно, где она существует), задающая ориентацию S, и пусть край поверхности Sсостоит из конечного числа кусочно гладких контуров. Через  обозначен край поверхности S, ориентированный с помощью единичного касательного к нему вектора
обозначен край поверхности S, ориентированный с помощью единичного касательного к нему вектора 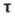 так, чтобы получающаяся ориентация края
так, чтобы получающаяся ориентация края  была согласована с ориентацией v поверхности S.
была согласована с ориентацией v поверхности S. 
 поверхности S)или, в координатном виде:
поверхности S)или, в координатном виде: 
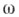 по ориентированному компактному многообразию Ми интеграла от самой формы
по ориентированному компактному многообразию Ми интеграла от самой формы  по ориентированному согласованно с ориентацией многообразия Мкраю
по ориентированному согласованно с ориентацией многообразия Мкраю  многообразия М:
многообразия М: