"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СТИНРОДА ЗАДАЧАЗначение СТИНРОДА ЗАДАЧА в математической энциклопедии:
- задача реализации циклов сингулярными многообразиями; поставлена Н. Стинродом (N. Steenrod, см. [1]). Пусть М - замкнутое ориентированное многообразие (топологическое, кусочно линейное, гладкое и т. д.), и пусть  - его ориентация (здесь Н п (М) -n -мсриая гомологии группа многообразия М). Любое непрерывное отображение - его ориентация (здесь Н п (М) -n -мсриая гомологии группа многообразия М). Любое непрерывное отображение  задает элемент задает элемент  С. з. состоит в описании тех гомологич. классов из X, называемых реализуемыми, к-рые получаются таким способом, т. е. имеют вид f*[M] для нeк-рых Миз данного класса. Все элементы групп Н 1 (Х)Н 2 (Х) реализуются. Лoбoй элемент группы Н п (Х), С. з. состоит в описании тех гомологич. классов из X, называемых реализуемыми, к-рые получаются таким способом, т. е. имеют вид f*[M] для нeк-рых Миз данного класса. Все элементы групп Н 1 (Х)Н 2 (Х) реализуются. Лoбoй элемент группы Н п (Х),  реализуется, но уже нек-рым отображением Пуанкаре комплекса Р. Кроме того, любой цикл можно реализовать псевдомногообразием. Можно также рассматривать неориентированные многообразия. реализуется, но уже нек-рым отображением Пуанкаре комплекса Р. Кроме того, любой цикл можно реализовать псевдомногообразием. Можно также рассматривать неориентированные многообразия.
Так, для гладких МС. з. состоит в описании образа гомоморфизма  где где  - группа ориентированных бордизмов пространства. Открытая Р. Томом (R. Thom, [2]) связь бордизмов - группа ориентированных бордизмов пространства. Открытая Р. Томом (R. Thom, [2]) связь бордизмов  с Тома пространствами MSO(k)прояснила С. з., сведя ее к изучению отображений с Тома пространствами MSO(k)прояснила С. з., сведя ее к изучению отображений 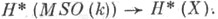 Был указан нереализуемый класс Был указан нереализуемый класс  где X - Эйленберга - Маклейна пространство где X - Эйленберга - Маклейна пространство  Для любого класса хнек-рые его кратные пх реализуются (гладкими многообразиями). Для любого класса хнек-рые его кратные пх реализуются (гладкими многообразиями). Лит.:[1] Еi1еnbеrg S., лAnn. Math.
|

 - его ориентация (здесь Н п (М) -n -мсриая гомологии группа многообразия М). Любое непрерывное отображение
- его ориентация (здесь Н п (М) -n -мсриая гомологии группа многообразия М). Любое непрерывное отображение  задает элемент
задает элемент  С. з. состоит в описании тех гомологич. классов из X, называемых реализуемыми, к-рые получаются таким способом, т. е. имеют вид f*[M] для нeк-рых Миз данного класса. Все элементы групп Н 1 (Х)Н 2 (Х) реализуются. Лoбoй элемент группы Н п (Х),
С. з. состоит в описании тех гомологич. классов из X, называемых реализуемыми, к-рые получаются таким способом, т. е. имеют вид f*[M] для нeк-рых Миз данного класса. Все элементы групп Н 1 (Х)Н 2 (Х) реализуются. Лoбoй элемент группы Н п (Х),  реализуется, но уже нек-рым отображением Пуанкаре комплекса Р. Кроме того, любой цикл можно реализовать псевдомногообразием. Можно также рассматривать неориентированные многообразия.
реализуется, но уже нек-рым отображением Пуанкаре комплекса Р. Кроме того, любой цикл можно реализовать псевдомногообразием. Можно также рассматривать неориентированные многообразия.  где
где  - группа ориентированных бордизмов пространства. Открытая Р. Томом (R. Thom, [2]) связь бордизмов
- группа ориентированных бордизмов пространства. Открытая Р. Томом (R. Thom, [2]) связь бордизмов  с Тома пространствами MSO(k)прояснила С. з., сведя ее к изучению отображений
с Тома пространствами MSO(k)прояснила С. з., сведя ее к изучению отображений 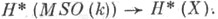 Был указан нереализуемый класс
Был указан нереализуемый класс  где X - Эйленберга - Маклейна пространство
где X - Эйленберга - Маклейна пространство  Для любого класса хнек-рые его кратные пх реализуются (гладкими многообразиями).
Для любого класса хнек-рые его кратные пх реализуются (гладкими многообразиями).