"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СТАТИСТИЧЕСКИЙ АНСАМБЛЬ
Значение СТАТИСТИЧЕСКИЙ АНСАМБЛЬ в математической энциклопедии:
- принятое в статистич. физике название фазового пространства (пространства состояний) какой-нибудь физич. системы вместе с нек-рым способом усреднения физич. величин (т. <н. наблюдаемых), связанных с этой системой. В случае классич. системы с фазовым пространством  наблюдаемые - действительные функции, определенные на
наблюдаемые - действительные функции, определенные на  а их усреднение происходит с помощью интегрирования по нек-рой вероятностной мере m на пространстве
а их усреднение происходит с помощью интегрирования по нек-рой вероятностной мере m на пространстве  В случае квантовой системы, описываемой векторами гильбертова пространства
В случае квантовой системы, описываемой векторами гильбертова пространства 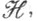 наблюдаемые задаются самосопряженными операторами, действующими в
наблюдаемые задаются самосопряженными операторами, действующими в  и усреднение вводится с помощью нек-рого положительного и нормированного функционала
и усреднение вводится с помощью нек-рого положительного и нормированного функционала  определенного на алгебре
определенного на алгебре  операторов, действующих в
операторов, действующих в  (такие функционалы на
(такие функционалы на  наз. состояниями). Обычно состояние задается в виде
наз. состояниями). Обычно состояние задается в виде

где  -положительный оператор в
-положительный оператор в  такой, что
такой, что  (оператор
(оператор 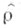 наз. матрицей плотности состояния
наз. матрицей плотности состояния 
Если задана эволюция физич. системы во времени (динамика системы), т. е. (в классич. случае) - группа  взаимно однозначных преобразовании фазового пространства в себя, порождаемая гамильтоновыми уравнениями движения с некрой функцией Гамильтона
взаимно однозначных преобразовании фазового пространства в себя, порождаемая гамильтоновыми уравнениями движения с некрой функцией Гамильтона  (энергия системы), или (в квантовом случае) - группа унитарных преобразований
(энергия системы), или (в квантовом случае) - группа унитарных преобразований  гильбертова пространства в себя, порождаемая оператором Гамильтона
гильбертова пространства в себя, порождаемая оператором Гамильтона  (оператором энергии системы), то естественно определяется эволюция во времени любого С. а., определенного для этой системы
(оператором энергии системы), то естественно определяется эволюция во времени любого С. а., определенного для этой системы

Для описания стационарного поведения системы рассматриваются равновесные ансамбли, т. е. меры или состояния, неизменные относительно эволюции (2). Хотя равновесных С. а., вообще говоря, много, в статистич. физике рассматривают только специальные - т. н. канонические ансамбли Гиббса (распределения).
Классические ансамбли Гиббса. Пусть, кроме гамильтониана  имеется нек-рый функционально независимый вместе с Н 0 набор
имеется нек-рый функционально независимый вместе с Н 0 набор  функций на
функций на  инвариантных относительно динамики Г t (в случае систем, состоящих из конечного, но произвольного числа частиц одного или нескольких видов,
инвариантных относительно динамики Г t (в случае систем, состоящих из конечного, но произвольного числа частиц одного или нескольких видов,  равно, напр., числу частиц какого-нибудь вида в конфигурации
равно, напр., числу частиц какого-нибудь вида в конфигурации  в случае системы магнитных диполей
в случае системы магнитных диполей  равно какой-нибудь составляющей их суммарного магнитного момента и т. д.). Большим канонич. ансамблем Гиббса наз. мера
равно какой-нибудь составляющей их суммарного магнитного момента и т. д.). Большим канонич. ансамблем Гиббса наз. мера

где  - мера, порождаемая симплектич. структурой на
- мера, порождаемая симплектич. структурой на  и v1, . . ., vk- действительные параметры, а
и v1, . . ., vk- действительные параметры, а  - нормировочный множитель, наз. большой статистической суммой:
- нормировочный множитель, наз. большой статистической суммой:

Мера  сосредоточенная на множестве
сосредоточенная на множестве

и совпадающая с условным распределением на этом множестве, порожденным мерой (3), наз. микроканонич. ансамблем Гиббса. Рассматриваются также и лпромежуточные

 наблюдаемые - действительные функции, определенные на
наблюдаемые - действительные функции, определенные на  а их усреднение происходит с помощью интегрирования по нек-рой вероятностной мере m на пространстве
а их усреднение происходит с помощью интегрирования по нек-рой вероятностной мере m на пространстве  В случае квантовой системы, описываемой векторами гильбертова пространства
В случае квантовой системы, описываемой векторами гильбертова пространства 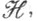 наблюдаемые задаются самосопряженными операторами, действующими в
наблюдаемые задаются самосопряженными операторами, действующими в  и усреднение вводится с помощью нек-рого положительного и нормированного функционала
и усреднение вводится с помощью нек-рого положительного и нормированного функционала  определенного на алгебре
определенного на алгебре  операторов, действующих в
операторов, действующих в  (такие функционалы на
(такие функционалы на  наз. состояниями). Обычно состояние задается в виде
наз. состояниями). Обычно состояние задается в виде 
 -положительный оператор в
-положительный оператор в  такой, что
такой, что  (оператор
(оператор 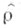 наз. матрицей плотности состояния
наз. матрицей плотности состояния 
 взаимно однозначных преобразовании фазового пространства в себя, порождаемая гамильтоновыми уравнениями движения с некрой функцией Гамильтона
взаимно однозначных преобразовании фазового пространства в себя, порождаемая гамильтоновыми уравнениями движения с некрой функцией Гамильтона  (энергия системы), или (в квантовом случае) - группа унитарных преобразований
(энергия системы), или (в квантовом случае) - группа унитарных преобразований  гильбертова пространства в себя, порождаемая оператором Гамильтона
гильбертова пространства в себя, порождаемая оператором Гамильтона  (оператором энергии системы), то естественно определяется эволюция во времени любого С. а., определенного для этой системы
(оператором энергии системы), то естественно определяется эволюция во времени любого С. а., определенного для этой системы 
 имеется нек-рый функционально независимый вместе с Н 0 набор
имеется нек-рый функционально независимый вместе с Н 0 набор  функций на
функций на  инвариантных относительно динамики Г t (в случае систем, состоящих из конечного, но произвольного числа частиц одного или нескольких видов,
инвариантных относительно динамики Г t (в случае систем, состоящих из конечного, но произвольного числа частиц одного или нескольких видов,  равно, напр., числу частиц какого-нибудь вида в конфигурации
равно, напр., числу частиц какого-нибудь вида в конфигурации  в случае системы магнитных диполей
в случае системы магнитных диполей  равно какой-нибудь составляющей их суммарного магнитного момента и т. д.). Большим канонич. ансамблем Гиббса наз. мера
равно какой-нибудь составляющей их суммарного магнитного момента и т. д.). Большим канонич. ансамблем Гиббса наз. мера 
 - мера, порождаемая симплектич. структурой на
- мера, порождаемая симплектич. структурой на  и v1, . . ., vk- действительные параметры, а
и v1, . . ., vk- действительные параметры, а  - нормировочный множитель, наз. большой статистической суммой:
- нормировочный множитель, наз. большой статистической суммой: 
 сосредоточенная на множестве
сосредоточенная на множестве 