"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СРАВНЕНИЕ ПО ПРОСТОМУ МОДУЛЮ
Значение СРАВНЕНИЕ ПО ПРОСТОМУ МОДУЛЮ в математической энциклопедии:
- сравнение, в к-ром модуль является простым числом. Отличительной чертой теории С. по п. м. является то, что классы вычетов по модулю . образуют конечное поле из рэлементов. Поэтому С. по п. м. можно трактовать как уравнения над простыми конечными полями и применять для их изучения, наряду с методами теории чисел, алгебро-геометрические методы.
Одним из основных вопросов теории сравнений от одного переменного х, имеющим важное значение в теории алгебраич. чисел, теории кодирования и других разделах математики, является вопрос об изучении законов разложения
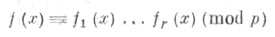
по простому модулю рпроизвольных целочисленных многочленов f(х)на неприводимые сомножители.
Основным вопросом теории С. по п. м. . от  переменных является вопрос о числе решений алгебраических сравнений
переменных является вопрос о числе решений алгебраических сравнений

когда  независимо друг от друга пробегают или все множество классов вычетов по модулю р(задачи на полную систему вычетов), или же нек-рую его собственную часть (задачи на неполную систему вычетов).
независимо друг от друга пробегают или все множество классов вычетов по модулю р(задачи на полную систему вычетов), или же нек-рую его собственную часть (задачи на неполную систему вычетов).
Первые результаты в исследовании вопроса о числе решений квадратичных и биквадратичных сравнений с двумя переменными были получены К. Гауссом [1] и Ж. Лагранжем [2]. Э. Артином [3] была установлена связь задачи о числе решений гиперэллиптич. сравнений  на полной системе вычетов по простому модулю рс гипотезой Римана для введенных им
на полной системе вычетов по простому модулю рс гипотезой Римана для введенных им 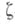 -функций полей алгебраич. функций с конечным полем констант. В частности, им была высказана гипотеза, что для числа Np решений сравнения
-функций полей алгебраич. функций с конечным полем констант. В частности, им была высказана гипотеза, что для числа Np решений сравнения 
 где многочлен f(х)=х n -а1 х n-1 +....+a п не является квадратом другого многочлена по модулю р, справедлива оценка
где многочлен f(х)=х n -а1 х n-1 +....+a п не является квадратом другого многочлена по модулю р, справедлива оценка

(здесь [х]- целая часть числа х).
Гипотеза Артина впервые была доказана X. Хассе [6] для случая эллиптич. сравнений

Позже А. Вейль [8] распространил метод Хассе на общий случай и получил для числа Nq решений уравнения f( х, y)=0 в элементах поля Fq, состоящего из q=pr элементов, где f( х, у) - абсолютно неприводимый многочлен с коэффициентами из Fq, оценку

Метод Хассе - Вейля сложен и требует привлечения современного аппарата абстрактной алгебраич. геометрии. В работе [7] найден простой и чисто арифметич. метод доказательства результатов Хассе - Вейля.
Менее изучены С. по п. м. от ппеременных. В качестве общего результата здесь можно указать следующую теорему. Пусть f(x1, . . ., х п )абсолютно неприводимый многочлен с целыми рациональными коэффициентами. Тогда для числа N р решений сравнения
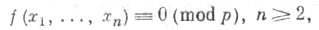
имеет место оценка

где константа с(f) не зависит от р. Более сильная оценка получена П. Делинем [9].
О С. по п. м. на неполной системе вычетов см. Виноградова гипотезы, Двучленное сравнение, Распределение степенных вычетов и невычетов.
Лит.:[1]Гаусс К. Ф., Труды по теории чисел, пер. с нем., М., 1959; [2] Lagrange J. L., Oeuvres, t. 3, P., 1869, p. 189-201; [3] Аrtin E., лMath. Zeitschrift

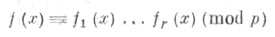
 переменных является вопрос о числе решений алгебраических сравнений
переменных является вопрос о числе решений алгебраических сравнений 
 независимо друг от друга пробегают или все множество классов вычетов по модулю р(задачи на полную систему вычетов), или же нек-рую его собственную часть (задачи на неполную систему вычетов).
независимо друг от друга пробегают или все множество классов вычетов по модулю р(задачи на полную систему вычетов), или же нек-рую его собственную часть (задачи на неполную систему вычетов).  на полной системе вычетов по простому модулю рс гипотезой Римана для введенных им
на полной системе вычетов по простому модулю рс гипотезой Римана для введенных им  -функций полей алгебраич. функций с конечным полем констант. В частности, им была высказана гипотеза, что для числа Np решений сравнения
-функций полей алгебраич. функций с конечным полем констант. В частности, им была высказана гипотеза, что для числа Np решений сравнения 
 где многочлен f(х)=х n -а1 х n-1 +....+a п не является квадратом другого многочлена по модулю р, справедлива оценка
где многочлен f(х)=х n -а1 х n-1 +....+a п не является квадратом другого многочлена по модулю р, справедлива оценка