"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПИНОРНАЯ ГРУППА
Значение СПИНОРНАЯ ГРУППА в математической энциклопедии:
невырожденной квадратичной формы Qна п-мерном  векторном пространстве Vнад полем k - связная линейная алгебраич. группа, являющаяся универсальной накрывающей неприводимой компоненты единицы
векторном пространстве Vнад полем k - связная линейная алгебраич. группа, являющаяся универсальной накрывающей неприводимой компоненты единицы  ортогональной группы On(Q)формы Q. Если char
ортогональной группы On(Q)формы Q. Если char  то группа
то группа  совпадает со специальной ортогональной группой SOn,(Q). С. <г. строится следующим образом. Пусть С=C(Q) - Клиффорда алгебра пары (V, Q), С + (соответственно С -) - подпространство в С, порожденное произведениями четного (соответственно нечетного) числа элементов из
совпадает со специальной ортогональной группой SOn,(Q). С. <г. строится следующим образом. Пусть С=C(Q) - Клиффорда алгебра пары (V, Q), С + (соответственно С -) - подпространство в С, порожденное произведениями четного (соответственно нечетного) числа элементов из 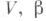 - канонич. антиавтоморфизм алгебры С, определяемый формулой
- канонич. антиавтоморфизм алгебры С, определяемый формулой

Вложение  позволяет определить группу Клиффорда
позволяет определить группу Клиффорда

и четную (или специальную) группу Клиффорда
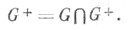
С. г. Spinn=Spinn(Q) определяется равенством

С. г. Spinn- простая (при  связная односвязная линейная алгебраич. группа типа В т при n=2 т+1 и типа Dm при
связная односвязная линейная алгебраич. группа типа В т при n=2 т+1 и типа Dm при  при n=6 это A3, а при n=4 это
при n=6 это A3, а при n=4 это  Имеют место изоморфизмы
Имеют место изоморфизмы

Линейное представление 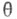 С. г. Spinn в пространстве V, определяемое равенством
С. г. Spinn в пространстве V, определяемое равенством  наз. ее векторным представлением. При этом
наз. ее векторным представлением. При этом

Группа Spinn; допускает также точное линейное представление (см. Спинорное представление).
Если  - поле действительных чисел,, а квадратичная форма Qположительно (или отрицательно) определена, то группа
- поле действительных чисел,, а квадратичная форма Qположительно (или отрицательно) определена, то группа  вещественных точек алгебраич. группы Spinn также наз. С. г. Это связная односвязная компактная группа Ли, являющаяся двулистной накрывающей специальной ортогональной группы
вещественных точек алгебраич. группы Spinn также наз. С. г. Это связная односвязная компактная группа Ли, являющаяся двулистной накрывающей специальной ортогональной группы 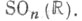 Имеют место изоморфизмы
Имеют место изоморфизмы

Лит.:[1] Вейль Г.,Классические группы, их инварианты и представления, пер. с англ., М., 1947; [2] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974; [3] Картан Э., Теория спиноров, пер. с франц., М., 1947; [4] IIостников М. М., Группы и алгебры Ли, М., 1982; [5] IIIевалле К., Теория групп Ли, пер. с англ., т. 1, М., 1948.
В. Л. Попов.

 векторном пространстве Vнад полем k - связная линейная алгебраич. группа, являющаяся универсальной накрывающей неприводимой компоненты единицы
векторном пространстве Vнад полем k - связная линейная алгебраич. группа, являющаяся универсальной накрывающей неприводимой компоненты единицы  ортогональной группы On(Q)формы Q. Если char
ортогональной группы On(Q)формы Q. Если char  то группа
то группа  совпадает со специальной ортогональной группой SOn,(Q). С. <г. строится следующим образом. Пусть С=C(Q) - Клиффорда алгебра пары (V, Q), С + (соответственно С -) - подпространство в С, порожденное произведениями четного (соответственно нечетного) числа элементов из
совпадает со специальной ортогональной группой SOn,(Q). С. <г. строится следующим образом. Пусть С=C(Q) - Клиффорда алгебра пары (V, Q), С + (соответственно С -) - подпространство в С, порожденное произведениями четного (соответственно нечетного) числа элементов из 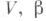 - канонич. антиавтоморфизм алгебры С, определяемый формулой
- канонич. антиавтоморфизм алгебры С, определяемый формулой 
 позволяет определить группу Клиффорда
позволяет определить группу Клиффорда 
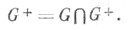

 связная односвязная линейная алгебраич. группа типа В т при n=2 т+1 и типа Dm при
связная односвязная линейная алгебраич. группа типа В т при n=2 т+1 и типа Dm при  при n=6 это A3, а при n=4 это
при n=6 это A3, а при n=4 это  Имеют место изоморфизмы
Имеют место изоморфизмы 
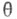 С. г. Spinn в пространстве V, определяемое равенством
С. г. Spinn в пространстве V, определяемое равенством  наз. ее векторным представлением. При этом
наз. ее векторным представлением. При этом 
 - поле действительных чисел,, а квадратичная форма Qположительно (или отрицательно) определена, то группа
- поле действительных чисел,, а квадратичная форма Qположительно (или отрицательно) определена, то группа  вещественных точек алгебраич. группы Spinn также наз. С. г. Это связная односвязная компактная группа Ли, являющаяся двулистной накрывающей специальной ортогональной группы
вещественных точек алгебраич. группы Spinn также наз. С. г. Это связная односвязная компактная группа Ли, являющаяся двулистной накрывающей специальной ортогональной группы 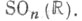 Имеют место изоморфизмы
Имеют место изоморфизмы 