"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНЫЙ СИНТЕЗЗначение СПЕКТРАЛЬНЫЙ СИНТЕЗ в математической энциклопедии:
восстановление инвариантных подпространств семейства линейных операторов по содержащимся в них собственным или корневым подпространствам этого семейства. Точнее, пусть 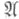 - коммутативное семейство операторов в топологическом векторном пространстве X, - коммутативное семейство операторов в топологическом векторном пространстве X,  - его точечный спектр, т. е. совокупность числовых функций - его точечный спектр, т. е. совокупность числовых функций  на на  для к-рых собственные подпространства для к-рых собственные подпространства 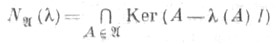
отличны от нулевого, 
корневые подпространства, соответствующие точкам 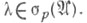 Подпространство Подпространство  инвариантное относительно инвариантное относительно 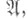 допускает С. с., если Lсовпадает с замыканием содержащихся в ном корневых подпространств. Если все допускает С. с., если Lсовпадает с замыканием содержащихся в ном корневых подпространств. Если все  -инвариантные подпространства допускают С. с., то говорят, что само семейство -инвариантные подпространства допускают С. с., то говорят, что само семейство 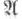 допускает С. с. допускает С. с.
Примером семейства, допускающего С. с., является всякая компактная коммутативная группа операторов в банаховом пространстве и, более общо, всякая группа с. относительно компактными траекториями. Если  то всякое одноэлементное семейство допускает С. с. ввиду существования жордннова разложения. В общем случае, для того чтобы оператор допускал С. с.., необходимо, по крайней мере, потребовать, чтобы все пространство Xдопускало С. <с. <относительно А, т. е. чтобы Аимел полную систему корневых подпространств. Условие полноты, однако, не обеспечивает возможности С. с. даже для нормальных операторов в гильбертовом пространстве; для того чтобы нормальный оператор Адопускал С. с., необходимо и достаточно, чтобы то всякое одноэлементное семейство допускает С. с. ввиду существования жордннова разложения. В общем случае, для того чтобы оператор допускал С. с.., необходимо, по крайней мере, потребовать, чтобы все пространство Xдопускало С. <с. <относительно А, т. е. чтобы Аимел полную систему корневых подпространств. Условие полноты, однако, не обеспечивает возможности С. с. даже для нормальных операторов в гильбертовом пространстве; для того чтобы нормальный оператор Адопускал С. с., необходимо и достаточно, чтобы 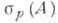 не содержал носителя меры, ортогональной многочленам. Ото условие выполняется тогда и только тогда, когда для любой области не содержал носителя меры, ортогональной многочленам. Ото условие выполняется тогда и только тогда, когда для любой области  найдется функция f, аналитическая в G, для к-рой найдется функция f, аналитическая в G, для к-рой 
В частности полные унитарные и полные самосопряженные операторы допускают С. с. Допускают С. с. и полные операторы, лблизкие
|

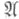 - коммутативное семейство операторов в топологическом векторном пространстве X,
- коммутативное семейство операторов в топологическом векторном пространстве X,  - его точечный спектр, т. е. совокупность числовых функций
- его точечный спектр, т. е. совокупность числовых функций  на
на  для к-рых собственные подпространства
для к-рых собственные подпространства 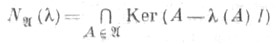

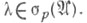 Подпространство
Подпространство  инвариантное относительно
инвариантное относительно 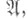 допускает С. с., если Lсовпадает с замыканием содержащихся в ном корневых подпространств. Если все
допускает С. с., если Lсовпадает с замыканием содержащихся в ном корневых подпространств. Если все  -инвариантные подпространства допускают С. с., то говорят, что само семейство
-инвариантные подпространства допускают С. с., то говорят, что само семейство 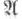 допускает С. с.
допускает С. с.  то всякое одноэлементное семейство допускает С. с. ввиду существования жордннова разложения. В общем случае, для того чтобы оператор допускал С. с.., необходимо, по крайней мере, потребовать, чтобы все пространство Xдопускало С. <с. <относительно А, т. е. чтобы Аимел полную систему корневых подпространств. Условие полноты, однако, не обеспечивает возможности С. с. даже для нормальных операторов в гильбертовом пространстве; для того чтобы нормальный оператор Адопускал С. с., необходимо и достаточно, чтобы
то всякое одноэлементное семейство допускает С. с. ввиду существования жордннова разложения. В общем случае, для того чтобы оператор допускал С. с.., необходимо, по крайней мере, потребовать, чтобы все пространство Xдопускало С. <с. <относительно А, т. е. чтобы Аимел полную систему корневых подпространств. Условие полноты, однако, не обеспечивает возможности С. с. даже для нормальных операторов в гильбертовом пространстве; для того чтобы нормальный оператор Адопускал С. с., необходимо и достаточно, чтобы 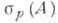 не содержал носителя меры, ортогональной многочленам. Ото условие выполняется тогда и только тогда, когда для любой области
не содержал носителя меры, ортогональной многочленам. Ото условие выполняется тогда и только тогда, когда для любой области  найдется функция f, аналитическая в G, для к-рой
найдется функция f, аналитическая в G, для к-рой 