|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНЫЙ ОПЕРАТОРЗначение СПЕКТРАЛЬНЫЙ ОПЕРАТОР в математической энциклопедии: - ограниченный линейный оператор А, отображающий банахово пространство Xв себяи такой, что для
Понятие С. о. можно распространить на неограниченные замкнутые операторы. При этом в 1) надо дополнительно потребовать, чтобы выполнялось включение
в
если ядро К(t, s) есть преобразование Фурье борелевской меры m на плоскости с полной вариацией var
суть ограниченные линейные операторы в
в случае сепарабельного Xточечный и остаточный спектры Ане более чем счетны и др. Лит.:[1] Данфорд Н., Шварц Дж., Линейные операторы, ч. 3- Спектральные операторы, пер. о англ., М., 1974; [2] Данфорд Н., лМатематика
|
|
|
|

 -алгебры
-алгебры  борелевских множеств
борелевских множеств  на плоскости существует разложение единицы
на плоскости существует разложение единицы  со свойствами: 1) для любого
со свойствами: 1) для любого  проектор
проектор  приводит А, т. с.
приводит А, т. с. и спектр
и спектр  лежит в
лежит в  где
где 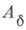 - сужение оператора Ана инвариантное подпространство
- сужение оператора Ана инвариантное подпространство  2) отображение
2) отображение  есть гомоморфизм
есть гомоморфизм  в булеву алгебру
в булеву алгебру  3) все проекторы
3) все проекторы  ограничены, т. е.
ограничены, т. е. 
 разложение единицы
разложение единицы  счетно аддитивно в сильной топологии пространства X, т. о. для любого
счетно аддитивно в сильной топологии пространства X, т. о. для любого  и любой последовательности
и любой последовательности 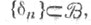 состоящей из попарно непересекающихся множеств,
состоящей из попарно непересекающихся множеств, 
 где D(А)- область определения оператора А, и
где D(А)- область определения оператора А, и  для ограниченных
для ограниченных 
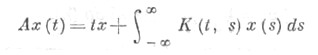
 на
на 
 и такое, что
и такое, что 

