"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНЫЕ ГОМОЛОГИИЗначение СПЕКТРАЛЬНЫЕ ГОМОЛОГИИ в математической энциклопедии:
- обратный предел 
групп гомологии с коэффициентами в абелевой группе Gнервов открытых покрытий  топологии, пространства X(они наз. также гомологиями Чеха, или Александрова - Чеха). Для замкнутого множества топологии, пространства X(они наз. также гомологиями Чеха, или Александрова - Чеха). Для замкнутого множества  группы группы  могут быть определены аналогичным образом с помощью подсистем могут быть определены аналогичным образом с помощью подсистем  всех тех множеств из всех тех множеств из  к-рые имеют непустое пересечение с А. Обратный предел групп пар к-рые имеют непустое пересечение с А. Обратный предел групп пар  G) наз. группой С. г. G) наз. группой С. г.  пары (X, А). Поскольку функтор обратного предела не сохраняет точность, гомологич. последовательность пары (X, А )вобщем случае не точна. Она полуточна в том смысле, что композиция любых двух отображений равна нулю. Для компактных Xпоследовательность оказывается точной в случае, когда G - компактная группа или иоле (в более общей ситуации - когда группа Gалгебраически компактна). С. г. непрерывны в том смысле, что пары (X, А). Поскольку функтор обратного предела не сохраняет точность, гомологич. последовательность пары (X, А )вобщем случае не точна. Она полуточна в том смысле, что композиция любых двух отображений равна нулю. Для компактных Xпоследовательность оказывается точной в случае, когда G - компактная группа или иоле (в более общей ситуации - когда группа Gалгебраически компактна). С. г. непрерывны в том смысле, что 
Отсутствие точности - не единственный недостаток С. г. Группы  оказываются неаддитивными в том смысле, что гомологии дискретного объединения оказываются неаддитивными в том смысле, что гомологии дискретного объединения   могут отличаться от прямой суммы могут отличаться от прямой суммы  G). От этого недостатка свободны спектральные гомологии G). От этого недостатка свободны спектральные гомологии  с компактными носителями, определяемые как прямой предел с компактными носителями, определяемые как прямой предел  взятый по всем компактным подмножествам взятый по всем компактным подмножествам  Естественность функтора Естественность функтора  подтверждается также тем, что любые обычные гомологии (симплициальные, клеточные, сингулярные) - это гомологии с компактными носителями. подтверждается также тем, что любые обычные гомологии (симплициальные, клеточные, сингулярные) - это гомологии с компактными носителями.
Несовпадение функторов  и и  - один из примеров того, как гомологии реагируют на логич. нюансы в их исходном определении (наоборот, когомологии проявляют в этом отношении значительную устойчивость). Среди логически возможных вариантов определения гомологии в общих категориях топологич. пространств правильный был отобран не сразу, в связи с чем ассоциированная с когомологиямв Александрова - Чеха теория гомологии - один из примеров того, как гомологии реагируют на логич. нюансы в их исходном определении (наоборот, когомологии проявляют в этом отношении значительную устойчивость). Среди логически возможных вариантов определения гомологии в общих категориях топологич. пространств правильный был отобран не сразу, в связи с чем ассоциированная с когомологиямв Александрова - Чеха теория гомологии  стала распространяться лишь в 60-е гг. (хотя первые определения были даны в 40-50-х гг.). Теория стала распространяться лишь в 60-е гг. (хотя первые определения были даны в 40-50-х гг.). Теория  удовлетворяет всем Стинрода - Эйленберга аксиомам (и является теорией с компактными носителями). Для компактных Xимеет место точная последовательность удовлетворяет всем Стинрода - Эйленберга аксиомам (и является теорией с компактными носителями). Для компактных Xимеет место точная последовательность 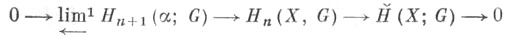
 - производный функтор обратного предела). В общем случае имеется эпиморфизм - производный функтор обратного предела). В общем случае имеется эпиморфизм  к-рый имеет нулевое ядро для любой алгебраически компактной группы G. Для любого гомологически локально связного (по отношению к к-рый имеет нулевое ядро для любой алгебраически компактной группы G. Для любого гомологически локально связного (по отношению к  локально компактного пространства функторы локально компактного пространства функторы  и и  изоморфны. изоморфны.
Лит.:[1] Стинрод Н., Эйленберг С., Основания алгебраической топологии, пер. с англ., М., 1958; [2] Скляренко Е. Г., лУспехи матем. наук
|


 топологии, пространства X(они наз. также гомологиями Чеха, или Александрова - Чеха). Для замкнутого множества
топологии, пространства X(они наз. также гомологиями Чеха, или Александрова - Чеха). Для замкнутого множества  группы
группы  могут быть определены аналогичным образом с помощью подсистем
могут быть определены аналогичным образом с помощью подсистем  всех тех множеств из
всех тех множеств из  к-рые имеют непустое пересечение с А. Обратный предел групп пар
к-рые имеют непустое пересечение с А. Обратный предел групп пар  G) наз. группой С. г.
G) наз. группой С. г.  пары (X, А). Поскольку функтор обратного предела не сохраняет точность, гомологич. последовательность пары (X, А )вобщем случае не точна. Она полуточна в том смысле, что композиция любых двух отображений равна нулю. Для компактных Xпоследовательность оказывается точной в случае, когда G - компактная группа или иоле (в более общей ситуации - когда группа Gалгебраически компактна). С. г. непрерывны в том смысле, что
пары (X, А). Поскольку функтор обратного предела не сохраняет точность, гомологич. последовательность пары (X, А )вобщем случае не точна. Она полуточна в том смысле, что композиция любых двух отображений равна нулю. Для компактных Xпоследовательность оказывается точной в случае, когда G - компактная группа или иоле (в более общей ситуации - когда группа Gалгебраически компактна). С. г. непрерывны в том смысле, что 
 оказываются неаддитивными в том смысле, что гомологии дискретного объединения
оказываются неаддитивными в том смысле, что гомологии дискретного объединения 
 могут отличаться от прямой суммы
могут отличаться от прямой суммы  G). От этого недостатка свободны спектральные гомологии
G). От этого недостатка свободны спектральные гомологии  с компактными носителями, определяемые как прямой предел
с компактными носителями, определяемые как прямой предел  взятый по всем компактным подмножествам
взятый по всем компактным подмножествам  Естественность функтора
Естественность функтора  подтверждается также тем, что любые обычные гомологии (симплициальные, клеточные, сингулярные) - это гомологии с компактными носителями.
подтверждается также тем, что любые обычные гомологии (симплициальные, клеточные, сингулярные) - это гомологии с компактными носителями.  и
и  - один из примеров того, как гомологии реагируют на логич. нюансы в их исходном определении (наоборот, когомологии проявляют в этом отношении значительную устойчивость). Среди логически возможных вариантов определения гомологии в общих категориях топологич. пространств правильный был отобран не сразу, в связи с чем ассоциированная с когомологиямв Александрова - Чеха теория гомологии
- один из примеров того, как гомологии реагируют на логич. нюансы в их исходном определении (наоборот, когомологии проявляют в этом отношении значительную устойчивость). Среди логически возможных вариантов определения гомологии в общих категориях топологич. пространств правильный был отобран не сразу, в связи с чем ассоциированная с когомологиямв Александрова - Чеха теория гомологии  стала распространяться лишь в 60-е гг. (хотя первые определения были даны в 40-50-х гг.). Теория
стала распространяться лишь в 60-е гг. (хотя первые определения были даны в 40-50-х гг.). Теория  удовлетворяет всем Стинрода - Эйленберга аксиомам (и является теорией с компактными носителями). Для компактных Xимеет место точная последовательность
удовлетворяет всем Стинрода - Эйленберга аксиомам (и является теорией с компактными носителями). Для компактных Xимеет место точная последовательность 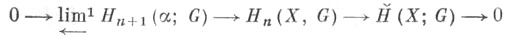
 - производный функтор обратного предела). В общем случае имеется эпиморфизм
- производный функтор обратного предела). В общем случае имеется эпиморфизм  к-рый имеет нулевое ядро для любой алгебраически компактной группы G. Для любого гомологически локально связного (по отношению к
к-рый имеет нулевое ядро для любой алгебраически компактной группы G. Для любого гомологически локально связного (по отношению к  локально компактного пространства функторы
локально компактного пространства функторы  и
и  изоморфны.
изоморфны.