"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНАЯ ТЕОРИЯ
Значение СПЕКТРАЛЬНАЯ ТЕОРИЯ в математической энциклопедии:
линейных операторов - раздел функционального анализа, изучающий структуру линейного оператора на основании свойств его спектральных характеристик (расположения спектра, поведения резольвенты, асимптотики собственных значений и т. д.). При этом под описанием структуры оператора может пониматься нахождение эквивалентного ему оператора в фиксированном классе конкретных (часто функциональных) моделей; определенный способ его восстановления из совокупности более простых операторов (напр., в форме прямой суммы или прямого интеграла); отыскание базиса, в к-ром матрица оператора имеет наиболее простой вид, доказательство полноты системы корневых векторов; полное описание решетки инвариантных подпространств, выделение максимальных цепочек инвариантных подпространств (треугольное представление); построение достаточно широкого функционального исчисления и т. д.
Весьма популярна (и плодотворна) в С. т. идея разложения оператора в прямую сумму операторов, соответствующую разбиению его спектра. Первые (для пространств бесконечной размерности) результаты такого рода получил Ф. Рисс (F. Riesz, 1909), предложивший следующую конструкцию. Пусть Т - ограниченный линейный оператор в банаховом пространстве X,  -его спектр,
-его спектр,  - его резольвента (т. е.
- его резольвента (т. е.

тогда формула

где Г - произвольный контур, охватывающий  определяет функциональное исчисление на алгебре ростков голоморфных функций в окрестности
определяет функциональное исчисление на алгебре ростков голоморфных функций в окрестности 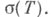 Если
Если  - открыто-замкнутое подмножество
- открыто-замкнутое подмножество  и f- функция, равная 1 в окрестности
и f- функция, равная 1 в окрестности  и 0 в окрестности
и 0 в окрестности  то получается проектор
то получается проектор  перестановочный с Т итакой, что
перестановочный с Т итакой, что 
Более общая С. т. основывается на понятии спектрального подпространства. Спектральным многообразием оператора Т, соответствующим замкнутому подмножеству  наз. совокупность
наз. совокупность  всех векторов
всех векторов  имеющих в
имеющих в  локальную резольвенту (т. е. аналитическую Х-значную функцию
локальную резольвенту (т. е. аналитическую Х-значную функцию  удовлетворяющую условию
удовлетворяющую условию 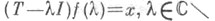
 спектральное подпространство - это замыкание спектрального многообразия. Если любые две локальные резольвенты одного и того же вектора совпадают на пересечения областей их определения (это означает, что локальная резольвента нулевого вектора равна нулю - условие, выполненное, напр., для всех операторов без собственных значений), то говорят, что оператор имеет свойство однозначного распространения. В этом случае для каждого
спектральное подпространство - это замыкание спектрального многообразия. Если любые две локальные резольвенты одного и того же вектора совпадают на пересечения областей их определения (это означает, что локальная резольвента нулевого вектора равна нулю - условие, выполненное, напр., для всех операторов без собственных значений), то говорят, что оператор имеет свойство однозначного распространения. В этом случае для каждого  определена локальная резольвента с максимальной областью определения, дополнение к к-рон наз. л о-кальным спектром оператора Тна векторе хи обозначается
определена локальная резольвента с максимальной областью определения, дополнение к к-рон наз. л о-кальным спектром оператора Тна векторе хи обозначается 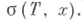 Таким образом, для оператора Т, обладающего свойством однозначного распространения,
Таким образом, для оператора Т, обладающего свойством однозначного распространения,

если при этом  замкнуто, то
замкнуто, то 
В общем случае аналогичное включение для спектральных подпространств не выполнено. Спектральные подпространства удовлетворяют условию дуальности

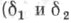 - непересекающиеся замкнутые множества), однако другое естественное условие
- непересекающиеся замкнутые множества), однако другое естественное условие 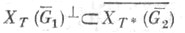 (G1 и G2 открыты,
(G1 и G2 открыты,  может нарушаться. Это включение становится справедливым, если его правую часть заменить лслабым спектральным подпространством
может нарушаться. Это включение становится справедливым, если его правую часть заменить лслабым спектральным подпространством

 -его спектр,
-его спектр,  - его резольвента (т. е.
- его резольвента (т. е. 

 определяет функциональное исчисление на алгебре ростков голоморфных функций в окрестности
определяет функциональное исчисление на алгебре ростков голоморфных функций в окрестности 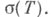 Если
Если  - открыто-замкнутое подмножество
- открыто-замкнутое подмножество  и f- функция, равная 1 в окрестности
и f- функция, равная 1 в окрестности  и 0 в окрестности
и 0 в окрестности  то получается проектор
то получается проектор  перестановочный с Т итакой, что
перестановочный с Т итакой, что 
 наз. совокупность
наз. совокупность  всех векторов
всех векторов  имеющих в
имеющих в  локальную резольвенту (т. е. аналитическую Х-значную функцию
локальную резольвенту (т. е. аналитическую Х-значную функцию  удовлетворяющую условию
удовлетворяющую условию 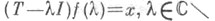
 спектральное подпространство - это замыкание спектрального многообразия. Если любые две локальные резольвенты одного и того же вектора совпадают на пересечения областей их определения (это означает, что локальная резольвента нулевого вектора равна нулю - условие, выполненное, напр., для всех операторов без собственных значений), то говорят, что оператор имеет свойство однозначного распространения. В этом случае для каждого
спектральное подпространство - это замыкание спектрального многообразия. Если любые две локальные резольвенты одного и того же вектора совпадают на пересечения областей их определения (это означает, что локальная резольвента нулевого вектора равна нулю - условие, выполненное, напр., для всех операторов без собственных значений), то говорят, что оператор имеет свойство однозначного распространения. В этом случае для каждого  определена локальная резольвента с максимальной областью определения, дополнение к к-рон наз. л о-кальным спектром оператора Тна векторе хи обозначается
определена локальная резольвента с максимальной областью определения, дополнение к к-рон наз. л о-кальным спектром оператора Тна векторе хи обозначается 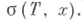 Таким образом, для оператора Т, обладающего свойством однозначного распространения,
Таким образом, для оператора Т, обладающего свойством однозначного распространения, 
 замкнуто, то
замкнуто, то 

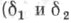 - непересекающиеся замкнутые множества), однако другое естественное условие
- непересекающиеся замкнутые множества), однако другое естественное условие 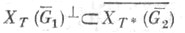 (G1 и G2 открыты,
(G1 и G2 открыты,  может нарушаться. Это включение становится справедливым, если его правую часть заменить лслабым спектральным подпространством
может нарушаться. Это включение становится справедливым, если его правую часть заменить лслабым спектральным подпространством