"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНАЯ ТЕОРИЯ
Значение СПЕКТРАЛЬНАЯ ТЕОРИЯ в математической энциклопедии:
дифференциальных операторов - раздел общей спектральной теории операторов, к-рый изучает спектральные свойства дифференциальных операторов в различных пространствах функций, особенно в гильбертовых пространствах измеримых функций.
Пусть  - область в
- область в  - ее граница,
- ее граница,

- линейный дифференциальный оператор (д. о.), и

- краевые условия, заданные линейными д. о. lj. Здесь

 - неотрицательные целые числа,
- неотрицательные целые числа, 
 а функции
а функции  и
и  определены в
определены в  и Г соответственно. В дальнейшем везде, где нет особых оговорок, предполагается, что
и Г соответственно. В дальнейшем везде, где нет особых оговорок, предполагается, что  и
и  -достаточно гладкие функции при n>1 и
-достаточно гладкие функции при n>1 и  при всех
при всех  если n = 1 и
если n = 1 и 
Самосопряженные расширения д. о. Пусть L'0 - д. о., к-рый задается выражением (1) на функциях из  т. е. имеющих производные любого порядка и обращающихся в нуль вне компакта, лежащего внутри
т. е. имеющих производные любого порядка и обращающихся в нуль вне компакта, лежащего внутри  Если для любой пары функций и(х)и v(х)из
Если для любой пары функций и(х)и v(х)из 

то L'0 наз. симметрическим д. о., а l - формально самосопряженным д. о. Пусть L0- замыкание д. о. L'0 в  Тогда д. о. L0 и сопряженный к нему L0 соответственно наз. минимальным и максимальным операторами, порожденными l(x, D); L*0 - расширение д. о. L0. Важной задачей теории д. о. является описание L0 и L*0. а также всех самосопряженных расширений д. о. L0.
Тогда д. о. L0 и сопряженный к нему L0 соответственно наз. минимальным и максимальным операторами, порожденными l(x, D); L*0 - расширение д. о. L0. Важной задачей теории д. о. является описание L0 и L*0. а также всех самосопряженных расширений д. о. L0.
Здесь можно применять абстрактную теорию расширений симметрич. операторов. Однако для д. о. самосопряженные расширения часто удается описать в терминах граничных условий.
Пусть

- дефектные подпространства оператора L0. Если dim  то L0=L*0, и д. о. L*0 наз. существенно самосопряженным. Любые из следующих условий достаточны для существенной самосопряженности д. о. L'0 в
то L0=L*0, и д. о. L*0 наз. существенно самосопряженным. Любые из следующих условий достаточны для существенной самосопряженности д. о. L'0 в  Формально самосопряженный д. о. l(x, D )имеет вид
Формально самосопряженный д. о. l(x, D )имеет вид

с действительными коэффициентами, и L'0 ограничен снизу; имеет вид (5), является эллиптическим, aik- постоянные,  монотонно не убывает и интеграл
монотонно не убывает и интеграл

имеет постоянные и действительные коэффициенты; имеет ограниченные коэффициенты, а главный член - эллиптич. типа с действительными и постоянными коэффициентами.
Пусть д. о. L0 имеет конечные индексы дефекта 
 что является характерным для обыкновенных д. о. В этом случае числа
что является характерным для обыкновенных д. о. В этом случае числа  совпадают с размерностями подпространств решений уравнений
совпадают с размерностями подпространств решений уравнений  из L2(a, b). Поэтому
из L2(a, b). Поэтому  и вычисление индексов дефекта д. о. связано с качественной теорией и асимптотич. методами обыкновенных дифференциальных уравнений.
и вычисление индексов дефекта д. о. связано с качественной теорией и асимптотич. методами обыкновенных дифференциальных уравнений.
Пусть  Если
Если 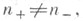 то д. о. L'0 не имеет ни одного самосопряженного расширения. Если n+ = n- = k, то для самосопряженности расширений д. о. L'0 надо задавать kграничных условий и они полностью описаны. Граничные условия принимают простой вид, когда выражение L'0 имеет два регулярных конца или имеет один регулярный конец, но т= =2k,
то д. о. L'0 не имеет ни одного самосопряженного расширения. Если n+ = n- = k, то для самосопряженности расширений д. о. L'0 надо задавать kграничных условий и они полностью описаны. Граничные условия принимают простой вид, когда выражение L'0 имеет два регулярных конца или имеет один регулярный конец, но т= =2k,  Конец аназ. регулярны м, если
Конец аназ. регулярны м, если  и
и  суммируемы на
суммируемы на  при любом
при любом 
Имеются примеры д. о. с частными производными в  с разрывными коэффициентами и с конечными индексами дефекта, но их теория еще слабо развита. В терминах граничных условий описаны не все самосопряженные расширения симметрии, д. о. с частными производными в ограниченной области, но описаны разнообразные расширения с заданными свойствами.
с разрывными коэффициентами и с конечными индексами дефекта, но их теория еще слабо развита. В терминах граничных условий описаны не все самосопряженные расширения симметрии, д. о. с частными производными в ограниченной области, но описаны разнообразные расширения с заданными свойствами.
Пусть l - формально самосопряженный эллиптический д. о. четного порядка т =2k с действительными коэффициентами,  - множество всех функций, имеющих производные любого порядка в ограниченной замкнутой области
- множество всех функций, имеющих производные любого порядка в ограниченной замкнутой области  и удовлетворяющих краевым условиям типа Дирихле
и удовлетворяющих краевым условиям типа Дирихле  Тогда д. о., определенный выражением lс областью определения
Тогда д. о., определенный выражением lс областью определения  является симметрическим, а его замыкание Lm- самосопряженным. Имеются другие примеры конкретных самосопряженных краевых условий для д. о., из них наиболее полно изучены д. о. 2-го порядка с краевыми условиями типа Дирихле. Неймана и третьего рода.
является симметрическим, а его замыкание Lm- самосопряженным. Имеются другие примеры конкретных самосопряженных краевых условий для д. о., из них наиболее полно изучены д. о. 2-го порядка с краевыми условиями типа Дирихле. Неймана и третьего рода.
Спектральный анализ самосопряженного д. о. Всякий самосопряженный д. о. Lдопускает спектральное разложение вида

где  - разложение единицы (ортогональное семейство проекторов). Однако общая формула не дает непосредственного разложения по собственным функциям конкретных самосопряженных д. о., и поэтому важно уметь семейство
- разложение единицы (ортогональное семейство проекторов). Однако общая формула не дает непосредственного разложения по собственным функциям конкретных самосопряженных д. о., и поэтому важно уметь семейство  выразить с помощью собственных функций. Если самосопряженный д. о. . имеет дискретный спектр
выразить с помощью собственных функций. Если самосопряженный д. о. . имеет дискретный спектр  с соответствующими ортонормированными собственными функциями
с соответствующими ортонормированными собственными функциями  то
то  - интегральный оператор с (спектральным) ядром
- интегральный оператор с (спектральным) ядром

При наличии непрерывного спектра у д. о. вопрос становится сложным: для непрерывного спектра нет собственных функции из  Однако имеют место следующие результаты.
Однако имеют место следующие результаты.
Пусть L - самосопряженный обыкновенный д. о. вида (1) в  - фундаментальная система решений уравнения
- фундаментальная система решений уравнения  Тогда существует монотонная матричная функция
Тогда существует монотонная матричная функция  (спектральная мера) такая, что разложение единицы
(спектральная мера) такая, что разложение единицы  д. о. Lзадается ядром
д. о. Lзадается ядром

Далее, для любой функции f(х)из  интеграл
интеграл

сходится в пространстве вектор-функций 
 порожденном мерой
порожденном мерой  и обратно, интеграл
и обратно, интеграл

сходится к f(х)в  Если выражение (1) имеет один регулярный конец аи т =2k, а индексы дефекта
Если выражение (1) имеет один регулярный конец аи т =2k, а индексы дефекта  то функции
то функции  выбираются так, чтобы они образовали фундаментальную систему в классе решений уравнения
выбираются так, чтобы они образовали фундаментальную систему в классе решений уравнения  удовлетворяющих краевым условиям в а, и в этом случае порядок спектральной меры будет равен k.
удовлетворяющих краевым условиям в а, и в этом случае порядок спектральной меры будет равен k.
Пусть L - самосопряженный эллиптич. д. о. в  Тогда его разложение единицы Е - интегральный оператор с ядром
Тогда его разложение единицы Е - интегральный оператор с ядром  и существует неубывающая функция
и существует неубывающая функция  такая, что для любых чисел
такая, что для любых чисел  и
и  имеет место
имеет место

при этом при каждом  существует конечная или бесконечная система
существует конечная или бесконечная система  решений уравнения
решений уравнения 
 и
и

Для оператора Шрёдингера  при условии
при условии  ядро
ядро  явно выражается через решения задачи теории рассеяния.
явно выражается через решения задачи теории рассеяния.
Для произвольных самосопряженных д. о. с частными производными также справедливы формулы (10), (11), в этом случае  могут быть обобщенными функциями, но конечного порядка.
могут быть обобщенными функциями, но конечного порядка.
Характер сходимости разложения по собственным функциям д. о. и асимптотич. свойства спектрального ядра помогают в обосновании метода Фурье при решении уравнении математич. физики. Для обыкновенных д. о. имеет место следующий окончательный результат - теорема равносходимости: разложения заданной суммируемой функции по собственным функциям д. о., ограниченного снизу, и интеграл Фурье сходятся или расходятся в точке одновременно. Для д. о. с частными производными вопрос становится сложным.
Качественная теория спектра д. о. занимается изучением природы спектра в зависимости от поведении коэффициентов, геометрии области и граничных условий.
Имеется серия признаков дискретности спектра д. о. Наиболее общим является следующий критерий и его обобщения: если  то для дискретности спектра д. о., порожденного выражением lи = - и n+q(x). в
то для дискретности спектра д. о., порожденного выражением lи = - и n+q(x). в  необходимо и достаточно, чтобы для любого j>0
необходимо и достаточно, чтобы для любого j>0

Для д. о. с частными производными обобщение этого критерия принимает более сложный вид. Имеются другие, более простые признаки дискретности спектра д. о., напр, самосопряженный д. о., порожденный выражением (5), будет иметь дискретный спектр, если  при
при  самосопряженный д. о. Lm имеет дискретный спектр.
самосопряженный д. о. Lm имеет дискретный спектр.
Изучение природы спектра при наличии непрерывной части становится трудной задачей. Вот нек-рые результаты: 1) если обыкновенный д. о. определяется формально самосопряженным выражением (1) с периодич. коэффициентами на  с общим периодом, то его спектр непрерывный и состоит из последовательности непересекающихся интервалов, концы к-рых стремятся к
с общим периодом, то его спектр непрерывный и состоит из последовательности непересекающихся интервалов, концы к-рых стремятся к  или
или  2) если д. о. определяется выражением
2) если д. о. определяется выражением
 и lim q(x)=0,
и lim q(x)=0,  непрерывный спектр его заполняет
непрерывный спектр его заполняет  а отрицательный спектр дискретный и может иметь предельную точку в нуле. Если k=1,
а отрицательный спектр дискретный и может иметь предельную точку в нуле. Если k=1,
 и
и

то отрицательный спектр будет конечным (на непрерывном спектре нет собственных значений).
Природа спектра зависит также от граничных условий. В ограниченной области описаны конкретные граничные условия, при выполнении к-рых самосопряженный д. о. Лапласа имеет непрерывную часть спектра. Это - результат бесконечности индексов дефекта минимального д. о. Лапласа в области сграницей.
Функции от самосопряженного д. о. изучаются с целью решения смешанных задач для дифференциальных уравнений, а также для внутренних задач теории д. о. Пусть L - эллиптич. д. о. порядка т. Хорошо изучена резольвента  при
при  и функции ехр (-Lt )и
и функции ехр (-Lt )и  при t>0. Последние являются разрешающими операторами для обобщенного уравнения теплопроводности uf=-Lu, и (0, x)=f(x)и обобщенного волнового уравнения
при t>0. Последние являются разрешающими операторами для обобщенного уравнения теплопроводности uf=-Lu, и (0, x)=f(x)и обобщенного волнового уравнения  u(0,x)=f(x). Все три оператор-функции являются интегральными с ядрами
u(0,x)=f(x). Все три оператор-функции являются интегральными с ядрами  (функции Грина) соответственно. Формула
(функции Грина) соответственно. Формула

устанавливает связь между Rи К. Нек-рые свойства  если L - эллиптический самосопряженный д. о. порядка тв
если L - эллиптический самосопряженный д. о. порядка тв  то при р>п/2топератору
то при р>п/2топератору  отвечает ядро типа Карлемана; при р>n/т оператор
отвечает ядро типа Карлемана; при р>n/т оператор  является ядерным и поэтому
является ядерным и поэтому

где  - собственные значения д. о. L т. Имеются и другие признаки ядерности оператора
- собственные значения д. о. L т. Имеются и другие признаки ядерности оператора  в
в 
Аналитич. и асимптотич. свойства функций Грина дают полезную информацию о спектральных характеристиках д. о. L. Напр., если в (13) известно поведение  при
при  то применение тауберовых теорем позволяет найти асимптотику
то применение тауберовых теорем позволяет найти асимптотику  То же самое удается, если известна асимптотика S р ехр (-Lt )при
То же самое удается, если известна асимптотика S р ехр (-Lt )при  Асимптотика
Асимптотика  и K(x, у, t )устанавливается, напр., методом параметрикс, методом потенциалов и т. д. Так, на этом пути удалось найти асимптотику
и K(x, у, t )устанавливается, напр., методом параметрикс, методом потенциалов и т. д. Так, на этом пути удалось найти асимптотику  для обширного класса эллиптич. д. о.
для обширного класса эллиптич. д. о.
Для определения асимптотики спектрального ядра  эллиптич. д. о. оказалось эффективным изучение асимптотики ядра G( х, у, t )при
эллиптич. д. о. оказалось эффективным изучение асимптотики ядра G( х, у, t )при  с дальнейшим применением различных тауберовых теорем. В частности, при х=у,
с дальнейшим применением различных тауберовых теорем. В частности, при х=у,

Несамосопряженные д. о. Наиболее полные результаты имеются для обыкновенных д. о. на конечном отрезке. Пусть д. о. Lопределяется выражением (1) при n=1, а т (х)=1на функциях, имеющих ( т-1) абсолютно непрерывные производные и удовлетворяющие краевым условиям:

Здесь  и числа av, bv одновременно не равны нулю. Пусть краевые условия (2) являются регулярными. Таковыми будут краевые условия типа Штурма - Лиувилля
и числа av, bv одновременно не равны нулю. Пусть краевые условия (2) являются регулярными. Таковыми будут краевые условия типа Штурма - Лиувилля 
 и периодич. типа
и периодич. типа  Тогда д. о. Lимеет бесконечное число собственных значений, к-рые имеют точную асимптотику; система собственных и присоединенных функций д. о. Lполна в Lp(0,1); разложение функций f(x) из D(L)по собственным и присоединенным функциям д. о. . сходится равномерно на (0, 1). Факт полноты системы собственных и присоединенных функций имеет место также при нек-рых нерегулярных краевых условиях, в частности типа распадающихся
Тогда д. о. Lимеет бесконечное число собственных значений, к-рые имеют точную асимптотику; система собственных и присоединенных функций д. о. Lполна в Lp(0,1); разложение функций f(x) из D(L)по собственным и присоединенным функциям д. о. . сходится равномерно на (0, 1). Факт полноты системы собственных и присоединенных функций имеет место также при нек-рых нерегулярных краевых условиях, в частности типа распадающихся 
 однако сходимость разложения в ряд по собственным и присоединенным функциям справедлива только для узкого класса (l- аналитических) функций.
однако сходимость разложения в ряд по собственным и присоединенным функциям справедлива только для узкого класса (l- аналитических) функций.
Пусть L0- самосопряженный оператор в сепарабельном гильбертовом пространстве Н - имеет собственные значения  и при нек-ром р>0 оператор
и при нек-ром р>0 оператор  является ядерным. Пусть L1- другой оператор такой, что
является ядерным. Пусть L1- другой оператор такой, что  является вполне непрерывным. Тогда система собственных и присоединенных векторов оператора L0+L1 полна в . (теорема Келдыша). Применение этой теоремы дает классы д. о., к-рые имеют полную систему собственных и присоединенных функций.
является вполне непрерывным. Тогда система собственных и присоединенных векторов оператора L0+L1 полна в . (теорема Келдыша). Применение этой теоремы дает классы д. о., к-рые имеют полную систему собственных и присоединенных функций.
Пусть Lm- д. о. в  и
и

тогда система собственных и присоединенных функций для д. о. Lm+L1 полна в  Однако разложение функции в ряд по этой системе, вообще говоря, расходится и суммируется со скобками по обобщенному методу Абеля.
Однако разложение функции в ряд по этой системе, вообще говоря, расходится и суммируется со скобками по обобщенному методу Абеля.
Если область  неограничена, то для выполнения условий теоремы Келдыша надо налагать дополнительные условия на рост коэффициентных функций д. о.
неограничена, то для выполнения условий теоремы Келдыша надо налагать дополнительные условия на рост коэффициентных функций д. о.
Мало изучены несамосопряженные д. о. с непрерывной частью спектра. Это связано с тем, что для них нет аналога теоремы о спектральном разложении. Исключение составляет д. o., порожденный выражением  при
при  или
или  с комплекснозначной функцией q(x). Пусть
с комплекснозначной функцией q(x). Пусть  является решением уравнения
является решением уравнения  при
при  и удовлетворяет начальным условиям
и удовлетворяет начальным условиям 
 Пусть f1(x) и f2 (х) - финитные функции из
Пусть f1(x) и f2 (х) - финитные функции из  и
и

Тоща существует линейный функционал . на линейном топологич. пространстве Gтакой, что 

Пространство G- множество всех целых четных функций первого порядка роста конечного типа, суммируемых на действительной оси. Если  то Rявно вычисляется. В этом случае на непрерывном спектре появляются спектральные особенности - полюсы ядра резольвенты, к-рые не являются собственными значениями д. о. Спектральные особенности присущи несамосопряженным операторам и из-за них вопросы разложения (и его сходимость) по собственным функциям принимают более сложный характер. Для д. о.
то Rявно вычисляется. В этом случае на непрерывном спектре появляются спектральные особенности - полюсы ядра резольвенты, к-рые не являются собственными значениями д. о. Спектральные особенности присущи несамосопряженным операторам и из-за них вопросы разложения (и его сходимость) по собственным функциям принимают более сложный характер. Для д. о.

в  в предположении, что комплексная функция q(x)убывает экспоненциально, также найден вид спектрального разложения через решение задачи теории рассеяния с учетом влияния спектральных особенностей.
в предположении, что комплексная функция q(x)убывает экспоненциально, также найден вид спектрального разложения через решение задачи теории рассеяния с учетом влияния спектральных особенностей.
В обратных задачах спектрального анализа требуется определение д. о. по нек-рым спектральным характеристикам. Полностью решены задачи определения одномерных дифференциальных уравнении Шрёдингера и систем типа Дирака по спектрам различных расширений, по спектральной мере, по данным рассеяния, т. е. по асимптотич. поведению нормированных собственных функций, и т. д. Обратные задачи нашли приложение в интегрировании нелинейных уравнений.
С. т. дифференциальных операторов возникла в связи с исследованиями колебания струны и вызвала к жизни теорию ортогональных разложений (18-19 вв.). Систематич. изучение самосопряженного д. о. 2-го порядка на конечном отрезке начинается с 1830 (Штурма - Лиувилля задача) и в 19 в. было предметом многих исследований, в частности в связи с теорией специальных функций. Однако замкнутость системы собственных функций д. о. Штурма - Лиувилля была доказана только в 1896, тогда же изучен и характер сходимости разложения по собственным функциям. Теория сингулярных д. о. берет свое начало в 1909- 1910, когда было найдено спектральное разложение самосопряженного неограниченного д. о. 2-го порядка с произвольной структурой спектра и, по существу, введено понятие индекса дефекта и получены первые результаты по теории расширений. Интерес к сингулярным д. о. возрос с 1920 с возникновением квантовой механики. Систематич. исследование несамосопряженных сингулярных д. о. началось с 1950, когда были заложены основы теории операторных пучков и указан метод доказательства полноты системы собственных и присоединенных функций для д. о.
Лит.: [1] Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965; [2] Глазман И. М., Прямые методы качественного спектрального анализа сингулярных дифференциальных операторов, М., 1963; [3] Данфорд Н., Шварц Д ж. - Т., Линейные операторы, пер. с англ., ч. 2, М., 1966; [4] Като Т., Теория возмущений линейных операторов, пер. с англ., М., 1972; [5] Левитан Б. М., Саргсян И. С., Введение в спектральную теорию, М., 1970; [6] Марченко В. А., Спектральная теория операторов Штурма - Лиувилля, К., 1972; [7] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [8] Титчмарш Э. Ч., Разложения по собственным функциям, связанные с дифференциальными уравнениями второго порядка, пер. с англ., ч. 1-2, М., 1960-61; [9] Фаддеев Л. Д., лТр. Матем. ин-та АН СССР

 - область в
- область в  - ее граница,
- ее граница, 


 - неотрицательные целые числа,
- неотрицательные целые числа, 
 а функции
а функции  и
и  определены в
определены в  и Г соответственно. В дальнейшем везде, где нет особых оговорок, предполагается, что
и Г соответственно. В дальнейшем везде, где нет особых оговорок, предполагается, что  и
и  -достаточно гладкие функции при n>1 и
-достаточно гладкие функции при n>1 и  при всех
при всех  если n = 1 и
если n = 1 и 
 т. е. имеющих производные любого порядка и обращающихся в нуль вне компакта, лежащего внутри
т. е. имеющих производные любого порядка и обращающихся в нуль вне компакта, лежащего внутри  Если для любой пары функций и(х)и v(х)из
Если для любой пары функций и(х)и v(х)из 

 Тогда д. о. L0 и сопряженный к нему L0 соответственно наз. минимальным и максимальным операторами, порожденными l(x, D); L*0 - расширение д. о. L0. Важной задачей теории д. о. является описание L0 и L*0. а также всех самосопряженных расширений д. о. L0.
Тогда д. о. L0 и сопряженный к нему L0 соответственно наз. минимальным и максимальным операторами, порожденными l(x, D); L*0 - расширение д. о. L0. Важной задачей теории д. о. является описание L0 и L*0. а также всех самосопряженных расширений д. о. L0. 
 то L0=L*0, и д. о. L*0 наз. существенно самосопряженным. Любые из следующих условий достаточны для существенной самосопряженности д. о. L'0 в
то L0=L*0, и д. о. L*0 наз. существенно самосопряженным. Любые из следующих условий достаточны для существенной самосопряженности д. о. L'0 в  Формально самосопряженный д. о. l(x, D )имеет вид
Формально самосопряженный д. о. l(x, D )имеет вид 
 монотонно не убывает и интеграл
монотонно не убывает и интеграл 

 что является характерным для обыкновенных д. о. В этом случае числа
что является характерным для обыкновенных д. о. В этом случае числа  совпадают с размерностями подпространств решений уравнений
совпадают с размерностями подпространств решений уравнений  из L2(a, b). Поэтому
из L2(a, b). Поэтому  и вычисление индексов дефекта д. о. связано с качественной теорией и асимптотич. методами обыкновенных дифференциальных уравнений.
и вычисление индексов дефекта д. о. связано с качественной теорией и асимптотич. методами обыкновенных дифференциальных уравнений.  Если
Если 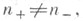 то д. о. L'0 не имеет ни одного самосопряженного расширения. Если n+ = n- = k, то для самосопряженности расширений д. о. L'0 надо задавать kграничных условий и они полностью описаны. Граничные условия принимают простой вид, когда выражение L'0 имеет два регулярных конца или имеет один регулярный конец, но т= =2k,
то д. о. L'0 не имеет ни одного самосопряженного расширения. Если n+ = n- = k, то для самосопряженности расширений д. о. L'0 надо задавать kграничных условий и они полностью описаны. Граничные условия принимают простой вид, когда выражение L'0 имеет два регулярных конца или имеет один регулярный конец, но т= =2k,  Конец аназ. регулярны м, если
Конец аназ. регулярны м, если  и
и  суммируемы на
суммируемы на  при любом
при любом 
 с разрывными коэффициентами и с конечными индексами дефекта, но их теория еще слабо развита. В терминах граничных условий описаны не все самосопряженные расширения симметрии, д. о. с частными производными в ограниченной области, но описаны разнообразные расширения с заданными свойствами.
с разрывными коэффициентами и с конечными индексами дефекта, но их теория еще слабо развита. В терминах граничных условий описаны не все самосопряженные расширения симметрии, д. о. с частными производными в ограниченной области, но описаны разнообразные расширения с заданными свойствами.  - множество всех функций, имеющих производные любого порядка в ограниченной замкнутой области
- множество всех функций, имеющих производные любого порядка в ограниченной замкнутой области  и удовлетворяющих краевым условиям типа Дирихле
и удовлетворяющих краевым условиям типа Дирихле  Тогда д. о., определенный выражением lс областью определения
Тогда д. о., определенный выражением lс областью определения  является симметрическим, а его замыкание Lm- самосопряженным. Имеются другие примеры конкретных самосопряженных краевых условий для д. о., из них наиболее полно изучены д. о. 2-го порядка с краевыми условиями типа Дирихле. Неймана и третьего рода.
является симметрическим, а его замыкание Lm- самосопряженным. Имеются другие примеры конкретных самосопряженных краевых условий для д. о., из них наиболее полно изучены д. о. 2-го порядка с краевыми условиями типа Дирихле. Неймана и третьего рода. 
 - разложение единицы (ортогональное семейство проекторов). Однако общая формула не дает непосредственного разложения по собственным функциям конкретных самосопряженных д. о., и поэтому важно уметь семейство
- разложение единицы (ортогональное семейство проекторов). Однако общая формула не дает непосредственного разложения по собственным функциям конкретных самосопряженных д. о., и поэтому важно уметь семейство  выразить с помощью собственных функций. Если самосопряженный д. о. . имеет дискретный спектр
выразить с помощью собственных функций. Если самосопряженный д. о. . имеет дискретный спектр  с соответствующими ортонормированными собственными функциями
с соответствующими ортонормированными собственными функциями  то
то  - интегральный оператор с (спектральным) ядром
- интегральный оператор с (спектральным) ядром 
 Однако имеют место следующие результаты.
Однако имеют место следующие результаты.  - фундаментальная система решений уравнения
- фундаментальная система решений уравнения  Тогда существует монотонная матричная функция
Тогда существует монотонная матричная функция  (спектральная мера) такая, что разложение единицы
(спектральная мера) такая, что разложение единицы  д. о. Lзадается ядром
д. о. Lзадается ядром 
 интеграл
интеграл 

 порожденном мерой
порожденном мерой  и обратно, интеграл
и обратно, интеграл 
 Если выражение (1) имеет один регулярный конец аи т =2k, а индексы дефекта
Если выражение (1) имеет один регулярный конец аи т =2k, а индексы дефекта  то функции
то функции  выбираются так, чтобы они образовали фундаментальную систему в классе решений уравнения
выбираются так, чтобы они образовали фундаментальную систему в классе решений уравнения  удовлетворяющих краевым условиям в а, и в этом случае порядок спектральной меры будет равен k.
удовлетворяющих краевым условиям в а, и в этом случае порядок спектральной меры будет равен k.  Тогда его разложение единицы Е - интегральный оператор с ядром
Тогда его разложение единицы Е - интегральный оператор с ядром  и существует неубывающая функция
и существует неубывающая функция  такая, что для любых чисел
такая, что для любых чисел  и
и  имеет место
имеет место 
 существует конечная или бесконечная система
существует конечная или бесконечная система  решений уравнения
решений уравнения 
 и
и 
 при условии
при условии  ядро
ядро  явно выражается через решения задачи теории рассеяния.
явно выражается через решения задачи теории рассеяния.  могут быть обобщенными функциями, но конечного порядка.
могут быть обобщенными функциями, но конечного порядка.  то для дискретности спектра д. о., порожденного выражением lи = - и n+q(x). в
то для дискретности спектра д. о., порожденного выражением lи = - и n+q(x). в  необходимо и достаточно, чтобы для любого j>0
необходимо и достаточно, чтобы для любого j>0 
 при
при  самосопряженный д. о. Lm имеет дискретный спектр.
самосопряженный д. о. Lm имеет дискретный спектр.  с общим периодом, то его спектр непрерывный и состоит из последовательности непересекающихся интервалов, концы к-рых стремятся к
с общим периодом, то его спектр непрерывный и состоит из последовательности непересекающихся интервалов, концы к-рых стремятся к  или
или  2) если д. о. определяется выражением
2) если д. о. определяется выражением  и lim q(x)=0,
и lim q(x)=0,  непрерывный спектр его заполняет
непрерывный спектр его заполняет  а отрицательный спектр дискретный и может иметь предельную точку в нуле. Если k=1,
а отрицательный спектр дискретный и может иметь предельную точку в нуле. Если k=1,
 и
и 
 при
при  и функции ехр (-Lt )и
и функции ехр (-Lt )и  при t>0. Последние являются разрешающими операторами для обобщенного уравнения теплопроводности uf=-Lu, и (0, x)=f(x)и обобщенного волнового уравнения
при t>0. Последние являются разрешающими операторами для обобщенного уравнения теплопроводности uf=-Lu, и (0, x)=f(x)и обобщенного волнового уравнения  u(0,x)=f(x). Все три оператор-функции являются интегральными с ядрами
u(0,x)=f(x). Все три оператор-функции являются интегральными с ядрами  (функции Грина) соответственно. Формула
(функции Грина) соответственно. Формула 
 если L - эллиптический самосопряженный д. о. порядка тв
если L - эллиптический самосопряженный д. о. порядка тв  то при р>п/2топератору
то при р>п/2топератору  отвечает ядро типа Карлемана; при р>n/т оператор
отвечает ядро типа Карлемана; при р>n/т оператор  является ядерным и поэтому
является ядерным и поэтому 
 - собственные значения д. о. L т. Имеются и другие признаки ядерности оператора
- собственные значения д. о. L т. Имеются и другие признаки ядерности оператора  в
в 
 при
при  то применение тауберовых теорем позволяет найти асимптотику
то применение тауберовых теорем позволяет найти асимптотику  То же самое удается, если известна асимптотика S р ехр (-Lt )при
То же самое удается, если известна асимптотика S р ехр (-Lt )при  Асимптотика
Асимптотика  и K(x, у, t )устанавливается, напр., методом параметрикс, методом потенциалов и т. д. Так, на этом пути удалось найти асимптотику
и K(x, у, t )устанавливается, напр., методом параметрикс, методом потенциалов и т. д. Так, на этом пути удалось найти асимптотику  для обширного класса эллиптич. д. о.
для обширного класса эллиптич. д. о.  эллиптич. д. о. оказалось эффективным изучение асимптотики ядра G( х, у, t )при
эллиптич. д. о. оказалось эффективным изучение асимптотики ядра G( х, у, t )при  с дальнейшим применением различных тауберовых теорем. В частности, при х=у,
с дальнейшим применением различных тауберовых теорем. В частности, при х=у,


 и числа av, bv одновременно не равны нулю. Пусть краевые условия (2) являются регулярными. Таковыми будут краевые условия типа Штурма - Лиувилля
и числа av, bv одновременно не равны нулю. Пусть краевые условия (2) являются регулярными. Таковыми будут краевые условия типа Штурма - Лиувилля 
 и периодич. типа
и периодич. типа  Тогда д. о. Lимеет бесконечное число собственных значений, к-рые имеют точную асимптотику; система собственных и присоединенных функций д. о. Lполна в Lp(0,1); разложение функций f(x) из D(L)по собственным и присоединенным функциям д. о. . сходится равномерно на (0, 1). Факт полноты системы собственных и присоединенных функций имеет место также при нек-рых нерегулярных краевых условиях, в частности типа распадающихся
Тогда д. о. Lимеет бесконечное число собственных значений, к-рые имеют точную асимптотику; система собственных и присоединенных функций д. о. Lполна в Lp(0,1); разложение функций f(x) из D(L)по собственным и присоединенным функциям д. о. . сходится равномерно на (0, 1). Факт полноты системы собственных и присоединенных функций имеет место также при нек-рых нерегулярных краевых условиях, в частности типа распадающихся 
 однако сходимость разложения в ряд по собственным и присоединенным функциям справедлива только для узкого класса (l- аналитических) функций.
однако сходимость разложения в ряд по собственным и присоединенным функциям справедлива только для узкого класса (l- аналитических) функций.  и при нек-ром р>0 оператор
и при нек-ром р>0 оператор  является ядерным. Пусть L1- другой оператор такой, что
является ядерным. Пусть L1- другой оператор такой, что  является вполне непрерывным. Тогда система собственных и присоединенных векторов оператора L0+L1 полна в . (теорема Келдыша). Применение этой теоремы дает классы д. о., к-рые имеют полную систему собственных и присоединенных функций.
является вполне непрерывным. Тогда система собственных и присоединенных векторов оператора L0+L1 полна в . (теорема Келдыша). Применение этой теоремы дает классы д. о., к-рые имеют полную систему собственных и присоединенных функций.  и
и 
 Однако разложение функции в ряд по этой системе, вообще говоря, расходится и суммируется со скобками по обобщенному методу Абеля.
Однако разложение функции в ряд по этой системе, вообще говоря, расходится и суммируется со скобками по обобщенному методу Абеля.  неограничена, то для выполнения условий теоремы Келдыша надо налагать дополнительные условия на рост коэффициентных функций д. о.
неограничена, то для выполнения условий теоремы Келдыша надо налагать дополнительные условия на рост коэффициентных функций д. о.  при
при  или
или  с комплекснозначной функцией q(x). Пусть
с комплекснозначной функцией q(x). Пусть  является решением уравнения
является решением уравнения  при
при  и удовлетворяет начальным условиям
и удовлетворяет начальным условиям 
 Пусть f1(x) и f2 (х) - финитные функции из
Пусть f1(x) и f2 (х) - финитные функции из  и
и 


 то Rявно вычисляется. В этом случае на непрерывном спектре появляются спектральные особенности - полюсы ядра резольвенты, к-рые не являются собственными значениями д. о. Спектральные особенности присущи несамосопряженным операторам и из-за них вопросы разложения (и его сходимость) по собственным функциям принимают более сложный характер. Для д. о.
то Rявно вычисляется. В этом случае на непрерывном спектре появляются спектральные особенности - полюсы ядра резольвенты, к-рые не являются собственными значениями д. о. Спектральные особенности присущи несамосопряженным операторам и из-за них вопросы разложения (и его сходимость) по собственным функциям принимают более сложный характер. Для д. о. 
 в предположении, что комплексная функция q(x)убывает экспоненциально, также найден вид спектрального разложения через решение задачи теории рассеяния с учетом влияния спектральных особенностей.
в предположении, что комплексная функция q(x)убывает экспоненциально, также найден вид спектрального разложения через решение задачи теории рассеяния с учетом влияния спектральных особенностей.