"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Значение СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ в математической энциклопедии:
последовательность дифференциальных модулей, каждый из к-рых является модулем гомологии предшествующего дифференциального модуля. Обычно рассматривают С. п. биградуированных (реже градуированных или триградуированных) модулей, к-рые изображают графически в виде наложенных друг на друга таблиц на плоскости. Более общо, рассматривают также С. п. объектов произвольной абелевой категории (напр., бимодулей, колец, алгебр, коалгебр, алгебр Хопфа и т. д.).
Все известные С. п. получаются из точных пар. Точной парой (D1,Е 1,i1,j1,k1) наз. точная диаграмма вида

Гомоморфизм dl=j1ki является дифференциалом в Е 1. По каждой точной паре можно построить производную точную пару (D2,E2,i2,y2,k2), для к-рой D2=Im i1 и E2=H(E1, d1). Итерирование этой конструкции дает С. п. Е={E п, dn}.
1) С. п. Лере. Фильтрованный цепной комплекс модулей ({К р}, d )определяет точную пару биградуированных модулей Dlp,q=Hp+q(KP), E1q,q=Hp+q(KP/KP-1). В ассоциированной С. п. бистепень дифференциала dr равна (-r, r-1) и
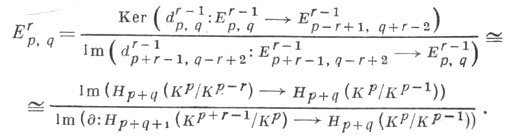
Модули  образуют фильтрацию в H*(K). Биградуированный модуль
образуют фильтрацию в H*(K). Биградуированный модуль

наз. присоединенным к Н * (К). Фильтрация {К р} наз. регулярной, если Kp=0 при р<0, 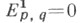 при q<0и
при q<0и  Для регулярной фильтрации
Для регулярной фильтрации 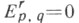 или р<0 или q<0; такая С. п. наз. С. п. первой четверти. Кроме того,
или р<0 или q<0; такая С. п. наз. С. п. первой четверти. Кроме того, 
 при r>max ( р,q+1). В этом случае говорят, что С. п. сходится к Н * (К), и пишут
при r>max ( р,q+1). В этом случае говорят, что С. п. сходится к Н * (К), и пишут 

2) С. п. Лере - Серра. Частный случай С. п. Лере возникает из цепного (или коцепного) комплекса фильтрованного топологич. пространства. Напр., фильтрация клеточного разбиения Xего остовами дает вырожденную С. п.  для к-рой
для к-рой 
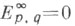 при
при  и
и  С. п. Лере - Серра получается из фильтрации тотального пространства . расслоения в смысле Серра
С. п. Лере - Серра получается из фильтрации тотального пространства . расслоения в смысле Серра 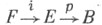 прообразами р -1( В п )остовов В п базы В. Если слой Fи база Влинейно связны, то для каждой группы коэффициентов G это дает С. п.
прообразами р -1( В п )остовов В п базы В. Если слой Fи база Влинейно связны, то для каждой группы коэффициентов G это дает С. п.  с дифференциалами dr бистепени ( - r, r-1), для к-рой
с дифференциалами dr бистепени ( - r, r-1), для к-рой

где  - система локальных коэффициентов над В, состоящая из групп Н q(F; G). При этом гомоморфизм
- система локальных коэффициентов над В, состоящая из групп Н q(F; G). При этом гомоморфизм 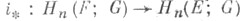 совпадает с композицией
совпадает с композицией

а гомоморфизм  совпадает с композицией
совпадает с композицией

где r достаточно велико. Дифференциал  С. п. совпадает с трансгрессией:
С. п. совпадает с трансгрессией:
Этой гомологич. С. п. Лере - Серра двойственна когомологич. С. п. Лере - Серра  с дифференциалами dr бистепени (r, -r+1), для к-рой
с дифференциалами dr бистепени (r, -r+1), для к-рой  Если Gявляется кольцом, токаждый член Е r является биградуированным кольцом, дифференциал dr является дифференцированием кольца Е r и умножение в Е r+1 индуцировано умножением в Е r. Если G - поле и база Водносвязна, то
Если Gявляется кольцом, токаждый член Е r является биградуированным кольцом, дифференциал dr является дифференцированием кольца Е r и умножение в Е r+1 индуцировано умножением в Е r. Если G - поле и база Водносвязна, то 

3) С. п. Атьи - Xирцебруха (- Уайтхеда ) получается применением функтора обобщенных (ко)гомологий  к той же фильтрации пространства Е. В ее когомологич. варианте
к той же фильтрации пространства Е. В ее когомологич. варианте 
 В отличие от С. п. Лере - Серра С. п. Атьи - Хирцебруха для тривиального расслоения
В отличие от С. п. Лере - Серра С. п. Атьи - Хирцебруха для тривиального расслоения  вообще говоря, невырождена.
вообще говоря, невырождена.
4) С. п. Эйленберга - Мура ассоциирована с каждым квадратом расслоений

В ее когомологич. варианте

Если R - поле и квадрат состоит из H-пространств и H-отображений, то эта С. п.- в категории биградуированных алгебр Хопфа.
5) С. п. Адамса  пишется для каждого простого
пишется для каждого простого  и любых пространств Xи Y(удовлетворяющих нек-рым условиям конечности). Для нее
и любых пространств Xи Y(удовлетворяющих нек-рым условиям конечности). Для нее

где А р - Стинрода алгебра rnod p. Бистепень dr равна (r, r-1). Эта С. п. сходится в том смысле, что при r>s существует мономорфизм  и, значит, определена группа
и, значит, определена группа  Существует такая убывающая фильтрация {Fs} группы {Y, X} стабильных гомотопич. классов отображении
Существует такая убывающая фильтрация {Fs} группы {Y, X} стабильных гомотопич. классов отображении  что
что  а
а  состоит из всех элементов группы {Y, X} конечного порядка, взаимно простого с р. Эта С. п. при Х=Y=S позволяет лв принципе
состоит из всех элементов группы {Y, X} конечного порядка, взаимно простого с р. Эта С. п. при Х=Y=S позволяет лв принципе


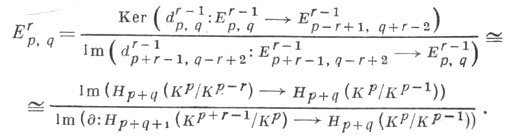
 образуют фильтрацию в H*(K). Биградуированный модуль
образуют фильтрацию в H*(K). Биградуированный модуль 
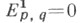 при q<0и
при q<0и  Для регулярной фильтрации
Для регулярной фильтрации 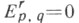 или р<0 или q<0; такая С. п. наз. С. п. первой четверти. Кроме того,
или р<0 или q<0; такая С. п. наз. С. п. первой четверти. Кроме того, 
 при r>max ( р,q+1). В этом случае говорят, что С. п. сходится к Н * (К), и пишут
при r>max ( р,q+1). В этом случае говорят, что С. п. сходится к Н * (К), и пишут 

 для к-рой
для к-рой 
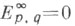 при
при  и
и  С. п. Лере - Серра получается из фильтрации тотального пространства . расслоения в смысле Серра
С. п. Лере - Серра получается из фильтрации тотального пространства . расслоения в смысле Серра 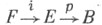 прообразами р -1( В п )остовов В п базы В. Если слой Fи база Влинейно связны, то для каждой группы коэффициентов G это дает С. п.
прообразами р -1( В п )остовов В п базы В. Если слой Fи база Влинейно связны, то для каждой группы коэффициентов G это дает С. п.  с дифференциалами dr бистепени ( - r, r-1), для к-рой
с дифференциалами dr бистепени ( - r, r-1), для к-рой 
 - система локальных коэффициентов над В, состоящая из групп Н q(F; G). При этом гомоморфизм
- система локальных коэффициентов над В, состоящая из групп Н q(F; G). При этом гомоморфизм 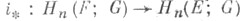 совпадает с композицией
совпадает с композицией 
 совпадает с композицией
совпадает с композицией 
 С. п. совпадает с трансгрессией:
С. п. совпадает с трансгрессией:
 с дифференциалами dr бистепени (r, -r+1), для к-рой
с дифференциалами dr бистепени (r, -r+1), для к-рой  Если Gявляется кольцом, токаждый член Е r является биградуированным кольцом, дифференциал dr является дифференцированием кольца Е r и умножение в Е r+1 индуцировано умножением в Е r. Если G - поле и база Водносвязна, то
Если Gявляется кольцом, токаждый член Е r является биградуированным кольцом, дифференциал dr является дифференцированием кольца Е r и умножение в Е r+1 индуцировано умножением в Е r. Если G - поле и база Водносвязна, то 

 к той же фильтрации пространства Е. В ее когомологич. варианте
к той же фильтрации пространства Е. В ее когомологич. варианте 
 В отличие от С. п. Лере - Серра С. п. Атьи - Хирцебруха для тривиального расслоения
В отличие от С. п. Лере - Серра С. п. Атьи - Хирцебруха для тривиального расслоения  вообще говоря, невырождена.
вообще говоря, невырождена. 

 пишется для каждого простого
пишется для каждого простого  и любых пространств Xи Y(удовлетворяющих нек-рым условиям конечности). Для нее
и любых пространств Xи Y(удовлетворяющих нек-рым условиям конечности). Для нее 
 и, значит, определена группа
и, значит, определена группа  Существует такая убывающая фильтрация {Fs} группы {Y, X} стабильных гомотопич. классов отображении
Существует такая убывающая фильтрация {Fs} группы {Y, X} стабильных гомотопич. классов отображении  что
что  а
а  состоит из всех элементов группы {Y, X} конечного порядка, взаимно простого с р. Эта С. п. при Х=Y=S позволяет лв принципе
состоит из всех элементов группы {Y, X} конечного порядка, взаимно простого с р. Эта С. п. при Х=Y=S позволяет лв принципе