"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СПЕКТР ДИНАМИЧЕСКОЙ СИСТЕМЫЗначение СПЕКТР ДИНАМИЧЕСКОЙ СИСТЕМЫ в математической энциклопедии:
{ Т t} с фазовым пространством Xи инвариантной мерой 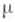 - общее название для различных спектральных инвариантов и спектральных свойств соответствующей группы (или полугруппы) унитарных (изометрических) операторов сдвига (Uif)(x) = f(Ttx )в гильбертовом пространстве - общее название для различных спектральных инвариантов и спектральных свойств соответствующей группы (или полугруппы) унитарных (изометрических) операторов сдвига (Uif)(x) = f(Ttx )в гильбертовом пространстве  Для динамич. системы в узком смысле слова - измеримого потока {Tt} или каскада {Т n}- речь идет о спектральных инвариантах одного нормального оператора:во втором случае - унитарного оператора (UTf) = f(Tx), а в первом - производящего самосопряженного оператора Аоднопараметрич. группы унитарных операторов {Ut} (согласно теореме Стоуна, Ut= е itA). Для динамич. системы в узком смысле слова - измеримого потока {Tt} или каскада {Т n}- речь идет о спектральных инвариантах одного нормального оператора:во втором случае - унитарного оператора (UTf) = f(Tx), а в первом - производящего самосопряженного оператора Аоднопараметрич. группы унитарных операторов {Ut} (согласно теореме Стоуна, Ut= е itA).
лСпектральная
|

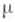 - общее название для различных спектральных инвариантов и спектральных свойств соответствующей группы (или полугруппы) унитарных (изометрических) операторов сдвига (Uif)(x) = f(Ttx )в гильбертовом пространстве
- общее название для различных спектральных инвариантов и спектральных свойств соответствующей группы (или полугруппы) унитарных (изометрических) операторов сдвига (Uif)(x) = f(Ttx )в гильбертовом пространстве  Для динамич. системы в узком смысле слова - измеримого потока {Tt} или каскада {Т n}- речь идет о спектральных инвариантах одного нормального оператора:во втором случае - унитарного оператора (UTf) = f(Tx), а в первом - производящего самосопряженного оператора Аоднопараметрич. группы унитарных операторов {Ut} (согласно теореме Стоуна, Ut= е itA).
Для динамич. системы в узком смысле слова - измеримого потока {Tt} или каскада {Т n}- речь идет о спектральных инвариантах одного нормального оператора:во втором случае - унитарного оператора (UTf) = f(Tx), а в первом - производящего самосопряженного оператора Аоднопараметрич. группы унитарных операторов {Ut} (согласно теореме Стоуна, Ut= е itA).