" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

СОФОКУСНЫЕ КРИВЫЕ

Значение СОФОКУСНЫЕ КРИВЫЕ в математической энциклопедии:

конфокальные кривые,- линии 2-го порядка, имеющие общие фокусы. Если Fи F' - две данные точки плоскости, то через каждую точку плоскости проходит один эллипс и одна гипербола, имеющие Fи F' своими фокусами (рис. 1).
Каждый эллипс ортогонален любой софокусной с ним гиперболе, т. е. пересекается с ней (в четырех точках) под прямым углом. Все множество софокусных эллипсов и гипербол в надлежащей системе координат определяется уравнением

где с - расстояние фокусов от начала координат, а - переменный параметр. При это уравнение определяет эллипс, при - гиперболу (при -мнимую линию 2-го порядка). Если один из фокусов стремится к бесконечности, то в пределе получаются два семейства софокусных парабол (рис. 2); любые две параболы, относящиеся к разным семействам, также ортогональны друг другу. При помощи софокусных эллипсов и гипербол на плоскости вводится система так наз. эллиптических координат.

Именно, если М( х, у) - произвольная точка плоскости, то, подставляя ее координаты х и ув уравнение (*), получают квадратное уравнение для корни его и наз. эллиптич. координатами точки М. Сами софокусные эллипсы и гиперболы составляют координатную сеть эллиптической координатной системы, т. е. определяются уравнениями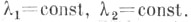
БСЭ-З.