|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СОПРЯЖЕННЫЙ КЛАСС ФУНКЦИИЗначение СОПРЯЖЕННЫЙ КЛАСС ФУНКЦИИ в математической энциклопедии: понятие теории функций, являющееся конкретным отображением двойственности в функциональных пространствах. Так, если класс функций Xрассматривается как банахово или топологическое векторное пространство, то С. к. ф. наз. класс функций, изометрически изоморфный сопряженному пространству X*. Напр., между пространствами
Если рассматривается нек-рый класс 2p-периодических суммируемых на
Класс функций, сопряженных к Lipa,
Лит.:[1] Freehet М., лС. r. Acad. sci.
|
|
|
|
и 
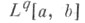при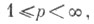 
существует изометрич. изоморфизм, при к-ром соответственные элементы х* и gсвязаны соотношением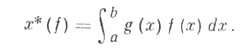 
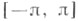функций X, то С. к. ф. наз. класс функций, сопряженных к функциям из X. Напр., класс функций, сопряженных к 
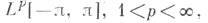совпадает с классом таких функций f из 
что 
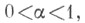совпадает с классом таких функций из Lipa, что 