" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

СОПРЯЖЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ

Значение СОПРЯЖЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ в математической энциклопедии:

к линейному преобразованию А - линейное преобразование А* евклидова. (или унитарного) пространства Lтакое, что для любых векторов . и уиз Lимеет место равенство скалярных произведений

(Ах, у)=( х, А *у).

С. л . п.- частный случай понятия сопряженного линейного отображения. Преобразование А* определяется по А единственным образом. Если Lконечномерно, то для всякого А существует С. л. п. А*, причем его матрица Вв базисе е ₁,...,е _п связана с матрицей Алинейного преобразования А в том же базисе соотношением 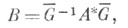где А*- сопряженная с А матрица, a G - Грама матрица базиса е ₁,...,е _п.
В евклидовом пространстве линейное преобразование А и его сопряженное А* имеют одинаковые харак-теристич. многочлены, равные определители, следы, одинаковые собственные значения. В унитарном пространстве их характеристич. многочлены, определители, следы, собственные значения комплексно сопряжены.
Т. С. Пиголкина.