"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СОПРЯЖЕННАЯ ФУНКЦИЯ
Значение СОПРЯЖЕННАЯ ФУНКЦИЯ в математической энциклопедии:
- понятие теории функций, являющееся конкретным отражением нек-рого инволютивного оператора для соответствующего класса функций.
1) С. ф. к комплекснозначной функции . наз. функцию  значения к-рой являются комплексно сопряженными к значениям f.
значения к-рой являются комплексно сопряженными к значениям f.
2) С. ф. к гармонической функции - см. Сопряженные гармонические функции.
3) С. ф. к  -периодической суммируемой на
-периодической суммируемой на 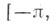
 функции f(x)наз. функцию
функции f(x)наз. функцию

она существует почти всюду и почти всюду совпадает с 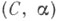 -суммой,
-суммой,  или суммой Абеля - Пуассона сопряженного тригонометрического ряда.
или суммой Абеля - Пуассона сопряженного тригонометрического ряда.
4) С. ф. к функции  определенной на векторном пространстве X, находящемся в двойственности (относительно билинейной формы <x,у>) с векторным пространством Y - функция на Y, задаваемая соотношением
определенной на векторном пространстве X, находящемся в двойственности (относительно билинейной формы <x,у>) с векторным пространством Y - функция на Y, задаваемая соотношением

Для функции, заданной на Y, сопряженная функция определяется аналогично.
С. ф. к функции одного переменного 
 будет функция
будет функция

С. ф. к функции  в гильбертовом пространстве Xсо скалярным произведением
в гильбертовом пространстве Xсо скалярным произведением  будет функция
будет функция  С. ф. к норме
С. ф. к норме  в нормированном пространстве будет функция N*(y), равная нулю, если
в нормированном пространстве будет функция N*(y), равная нулю, если  и равная
и равная  если
если 
Если f - гладкая растущая на бесконечности быстрее линейной функция, то f* - не что иное, как Лежандра преобразование функции f. Для одномерных строго выпуклых функций определение, равносильное (*), было дано У. Юнгом [1], в других терминах. У. Юнг определял С. ф. к функции

где 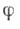 непрерывна и строго возрастает, соотношением
непрерывна и строго возрастает, соотношением

где  - функция, обратная к
- функция, обратная к  Определение (*) для одномерных функций было впервые предложено С. Мандельбройтом (S. Mandelbrojt), в конечномерном случае - В. Фенхелем [2], в бесконечномерном - Ж. Моро [3] и А. Брёнстедом [4]. Для выпуклой функции н сопряженной с ней выполнено неравенство Юнга
Определение (*) для одномерных функций было впервые предложено С. Мандельбройтом (S. Mandelbrojt), в конечномерном случае - В. Фенхелем [2], в бесконечномерном - Ж. Моро [3] и А. Брёнстедом [4]. Для выпуклой функции н сопряженной с ней выполнено неравенство Юнга

С. ф.- выпуклая замкнутая функция. Оператор сопряжения*:  однозначно отображает совокупность собственных выпуклых замкнутых функций на Xна совокупность собственных выпуклых замкнутых функций на Y (теорема Фенхеля - Моро).
однозначно отображает совокупность собственных выпуклых замкнутых функций на Xна совокупность собственных выпуклых замкнутых функций на Y (теорема Фенхеля - Моро).
Подробнее см. [5] и [6].
См. также Выпуклый анализ, Опорная функция, Двойственность в экстремальных задачах и выпуклом анализе.
Лит.:[1] Joung W. H., лProc. Roy. Soc. A

 значения к-рой являются комплексно сопряженными к значениям f.
значения к-рой являются комплексно сопряженными к значениям f.  -периодической суммируемой на
-периодической суммируемой на 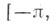
 функции f(x)наз. функцию
функции f(x)наз. функцию 
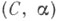 -суммой,
-суммой,  или суммой Абеля - Пуассона сопряженного тригонометрического ряда.
или суммой Абеля - Пуассона сопряженного тригонометрического ряда.  определенной на векторном пространстве X, находящемся в двойственности (относительно билинейной формы <x,у>) с векторным пространством Y - функция на Y, задаваемая соотношением
определенной на векторном пространстве X, находящемся в двойственности (относительно билинейной формы <x,у>) с векторным пространством Y - функция на Y, задаваемая соотношением 

 будет функция
будет функция 
 в гильбертовом пространстве Xсо скалярным произведением
в гильбертовом пространстве Xсо скалярным произведением  будет функция
будет функция  С. ф. к норме
С. ф. к норме  в нормированном пространстве будет функция N*(y), равная нулю, если
в нормированном пространстве будет функция N*(y), равная нулю, если  и равная
и равная  если
если 

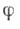 непрерывна и строго возрастает, соотношением
непрерывна и строго возрастает, соотношением 
 - функция, обратная к
- функция, обратная к  Определение (*) для одномерных функций было впервые предложено С. Мандельбройтом (S. Mandelbrojt), в конечномерном случае - В. Фенхелем [2], в бесконечномерном - Ж. Моро [3] и А. Брёнстедом [4]. Для выпуклой функции н сопряженной с ней выполнено неравенство Юнга
Определение (*) для одномерных функций было впервые предложено С. Мандельбройтом (S. Mandelbrojt), в конечномерном случае - В. Фенхелем [2], в бесконечномерном - Ж. Моро [3] и А. Брёнстедом [4]. Для выпуклой функции н сопряженной с ней выполнено неравенство Юнга 
 однозначно отображает совокупность собственных выпуклых замкнутых функций на Xна совокупность собственных выпуклых замкнутых функций на Y (теорема Фенхеля - Моро).
однозначно отображает совокупность собственных выпуклых замкнутых функций на Xна совокупность собственных выпуклых замкнутых функций на Y (теорема Фенхеля - Моро).