"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СОКРАЩЕННАЯ НОРМАЛЬНАЯ ФОРМАЗначение СОКРАЩЕННАЯ НОРМАЛЬНАЯ ФОРМА в математической энциклопедии:
булевой функции - дизъюнктивная нормальная форма (д. н. ф.), представляющая собой дизъюнкцию всех простых импликант данной функции. Конъюнкция  наз. импликантой булевой функции f, если справедливо соотношение наз. импликантой булевой функции f, если справедливо соотношение 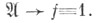 Импликанта наз. простой, если после вычеркивания из нее любой буквы она перестает быть импликантой. Построение С. н. ф. является первым этапом булевых функций минимизации, поскольку минимальная д. н. ф. получается из сокращенной удалением нек-рых импликант. Число конъюнкций в С. н. ф. характеризует трудоемкость выполнения этого этапа. Оценки этой величины (см. Булевых функций нормальные формы )показывают, что вообще говоря, С. н. ф. сложнее исходного задания функции; при переходе к С. н. ф. от совершенной сокращаются только длины конъюнкций, число же их значительно увеличивается. Кроме того, у лпочти всех Импликанта наз. простой, если после вычеркивания из нее любой буквы она перестает быть импликантой. Построение С. н. ф. является первым этапом булевых функций минимизации, поскольку минимальная д. н. ф. получается из сокращенной удалением нек-рых импликант. Число конъюнкций в С. н. ф. характеризует трудоемкость выполнения этого этапа. Оценки этой величины (см. Булевых функций нормальные формы )показывают, что вообще говоря, С. н. ф. сложнее исходного задания функции; при переходе к С. н. ф. от совершенной сокращаются только длины конъюнкций, число же их значительно увеличивается. Кроме того, у лпочти всех
|

 наз. импликантой булевой функции f, если справедливо соотношение
наз. импликантой булевой функции f, если справедливо соотношение 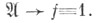 Импликанта наз. простой, если после вычеркивания из нее любой буквы она перестает быть импликантой. Построение С. н. ф. является первым этапом булевых функций минимизации, поскольку минимальная д. н. ф. получается из сокращенной удалением нек-рых импликант. Число конъюнкций в С. н. ф. характеризует трудоемкость выполнения этого этапа. Оценки этой величины (см. Булевых функций нормальные формы )показывают, что вообще говоря, С. н. ф. сложнее исходного задания функции; при переходе к С. н. ф. от совершенной сокращаются только длины конъюнкций, число же их значительно увеличивается. Кроме того, у лпочти всех
Импликанта наз. простой, если после вычеркивания из нее любой буквы она перестает быть импликантой. Построение С. н. ф. является первым этапом булевых функций минимизации, поскольку минимальная д. н. ф. получается из сокращенной удалением нек-рых импликант. Число конъюнкций в С. н. ф. характеризует трудоемкость выполнения этого этапа. Оценки этой величины (см. Булевых функций нормальные формы )показывают, что вообще говоря, С. н. ф. сложнее исходного задания функции; при переходе к С. н. ф. от совершенной сокращаются только длины конъюнкций, число же их значительно увеличивается. Кроме того, у лпочти всех