"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СОВЕРШЕННОЕ БИКОМПАКТНОЕ РАСШИРЕНИЕЗначение СОВЕРШЕННОЕ БИКОМПАКТНОЕ РАСШИРЕНИЕ в математической энциклопедии:
- расширение Y вполне регулярного пространства X такое, что замыкание в Yграницы любого открытого множества 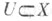 служит границей O(U), где O(U) - максимально открытое в У множество, для к-рого служит границей O(U), где O(U) - максимально открытое в У множество, для к-рого  Эквивалентные требования: а) Эквивалентные требования: а)  для любой пары непересекающихся открытых множеств U, V;б) если замкнутое множество Fразбивает Xна открытые множества . и V, то замыкание Fв Y разбивает Y на О(U)и О(V);в) ни в одной из своих точек для любой пары непересекающихся открытых множеств U, V;б) если замкнутое множество Fразбивает Xна открытые множества . и V, то замыкание Fв Y разбивает Y на О(U)и О(V);в) ни в одной из своих точек 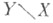 но разбивает Y локально. С. б. р. характеризуется также как монотонный образ Стоуна - Чеха бикомпактного расширения но разбивает Y локально. С. б. р. характеризуется также как монотонный образ Стоуна - Чеха бикомпактного расширения 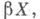 причем причем  в том и только в том случае является единственным С. б. р. X, когда в том и только в том случае является единственным С. б. р. X, когда 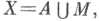 где А - бикомпакт, а dim М=0. Локальная связность Xвлечет локальную связность любого совершенного расширения Y с 1-й аксиомой счетности (а также расширений, предшествующих Y). Среди всех С. б. р. Xминимальное С. б. р. где А - бикомпакт, а dim М=0. Локальная связность Xвлечет локальную связность любого совершенного расширения Y с 1-й аксиомой счетности (а также расширений, предшествующих Y). Среди всех С. б. р. Xминимальное С. б. р.  существует тогда и только тогда, когда у Xимеется хотя бы одно расширение с пунктиформным наростом. Нарост в существует тогда и только тогда, когда у Xимеется хотя бы одно расширение с пунктиформным наростом. Нарост в  пунктиформен, причем пунктиформен, причем  является при этом максимальным среди всех расширений с пунктаформными наростами. Всякий гомеоморфизм Xраспространяется до гомеоморфизма является при этом максимальным среди всех расширений с пунктаформными наростами. Всякий гомеоморфизм Xраспространяется до гомеоморфизма  авсякое совершенное отображение Xна X' продолжается до отображения авсякое совершенное отображение Xна X' продолжается до отображения
 на на 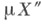 (при условии, что (при условии, что  существует). существует).
М. И. Войцеховский.
|

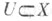 служит границей O(U), где O(U) - максимально открытое в У множество, для к-рого
служит границей O(U), где O(U) - максимально открытое в У множество, для к-рого  Эквивалентные требования: а)
Эквивалентные требования: а)
 для любой пары непересекающихся открытых множеств U, V;б) если замкнутое множество Fразбивает Xна открытые множества . и V, то замыкание Fв Y разбивает Y на О(U)и О(V);в) ни в одной из своих точек
для любой пары непересекающихся открытых множеств U, V;б) если замкнутое множество Fразбивает Xна открытые множества . и V, то замыкание Fв Y разбивает Y на О(U)и О(V);в) ни в одной из своих точек 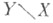 но разбивает Y локально. С. б. р. характеризуется также как монотонный образ Стоуна - Чеха бикомпактного расширения
но разбивает Y локально. С. б. р. характеризуется также как монотонный образ Стоуна - Чеха бикомпактного расширения 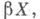 причем
причем  в том и только в том случае является единственным С. б. р. X, когда
в том и только в том случае является единственным С. б. р. X, когда 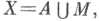 где А - бикомпакт, а dim М=0. Локальная связность Xвлечет локальную связность любого совершенного расширения Y с 1-й аксиомой счетности (а также расширений, предшествующих Y). Среди всех С. б. р. Xминимальное С. б. р.
где А - бикомпакт, а dim М=0. Локальная связность Xвлечет локальную связность любого совершенного расширения Y с 1-й аксиомой счетности (а также расширений, предшествующих Y). Среди всех С. б. р. Xминимальное С. б. р.  существует тогда и только тогда, когда у Xимеется хотя бы одно расширение с пунктиформным наростом. Нарост в
существует тогда и только тогда, когда у Xимеется хотя бы одно расширение с пунктиформным наростом. Нарост в  пунктиформен, причем
пунктиформен, причем  является при этом максимальным среди всех расширений с пунктаформными наростами. Всякий гомеоморфизм Xраспространяется до гомеоморфизма
является при этом максимальным среди всех расширений с пунктаформными наростами. Всякий гомеоморфизм Xраспространяется до гомеоморфизма  авсякое совершенное отображение Xна X' продолжается до отображения
авсякое совершенное отображение Xна X' продолжается до отображения  на
на 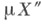 (при условии, что
(при условии, что  существует).
существует).