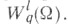"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СОБОЛЕВА ПРОСТРАНСТВО
Значение СОБОЛЕВА ПРОСТРАНСТВО в математической энциклопедии:
пространство  функций f=f(x)=f(x1,...,xn), определенных на множестве
функций f=f(x)=f(x1,...,xn), определенных на множестве  (обычно открытом) и интегрируемых с р- йстепенью их модуля вместе со своими обобщенными производными до порядка lвключительно
(обычно открытом) и интегрируемых с р- йстепенью их модуля вместе со своими обобщенными производными до порядка lвключительно 

Норма функции  определяется при помощи равенства
определяется при помощи равенства

Здесь

есть обобщенная частная производная от f порядка |k| = и норма
и норма
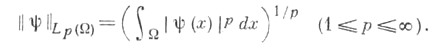
При  эта норма равна существенному максимуму:
эта норма равна существенному максимуму:

т. <е. нижней грани чисел А, для к-рых неравенство  имеет место на множестве меры нуль.
имеет место на множестве меры нуль.
Пространство Соболева  определено и впервые применено в теории краевых задач матeматич. физики в [1], [2].
определено и впервые применено в теории краевых задач матeматич. физики в [1], [2].
Благодаря тому что в определении С. п . участвуют не обычные, а обобщенные производные, оно является полным, т. е. банаховым пространством.
Наряду с  рассматривается его линейное подпространство, обозначенное
рассматривается его линейное подпространство, обозначенное  и состоящее из функций, имеющих равномерно непрерывные на
и состоящее из функций, имеющих равномерно непрерывные на  частные производные l- гопорядка. Подпространство
частные производные l- гопорядка. Подпространство  имеет преимущества перед
имеет преимущества перед  однако оно не замкнуто в метрике
однако оно не замкнуто в метрике  и само по себе не является полным пространством, но для широкого класса областей (с липшициевой границей, см. ниже) при
и само по себе не является полным пространством, но для широкого класса областей (с липшициевой границей, см. ниже) при  пространство
пространство  плотно в
плотно в  т. е. для таких областей пространство
т. е. для таких областей пространство  кроме полноты, приобретает новое свойство, заключающееся в том, что каждая принадлежащая к нему функция может быть как угодно хорошо приближена в метрике
кроме полноты, приобретает новое свойство, заключающееся в том, что каждая принадлежащая к нему функция может быть как угодно хорошо приближена в метрике  функциями из
функциями из 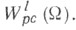
Выражение (1) для нормы функции  удобно заменить на следующее выражение:
удобно заменить на следующее выражение:

Норма (1') эквивалентна норме (1) (т. е.
 где c1, с 2>0 не зависят от f). При р=2 норма (1') гильбертова, и это широко используется в приложениях.
где c1, с 2>0 не зависят от f). При р=2 норма (1') гильбертова, и это широко используется в приложениях.
Граница Г ограниченной области  наз. липшицевой, если, какова бы ни была точка
наз. липшицевой, если, какова бы ни была точка  найдется прямоугольная система координат
найдется прямоугольная система координат 
 с началом в этой точке и прямоугольник
с началом в этой точке и прямоугольник

такой, что пересечение  описывается функцией
описывается функцией 

удовлетворяющей на  (проекции
(проекции  на плоскость
на плоскость  условию Липшица
условию Липшица

где константа Мне зависит от указанных точек 
 и
и  Гладкие и многие кусочно гладкие границы охватываются понятием липшицевой границы. Для области с липшицевой границей норма (1) эквивалентна следующей:
Гладкие и многие кусочно гладкие границы охватываются понятием липшицевой границы. Для области с липшицевой границей норма (1) эквивалентна следующей:

где полунорма

Можно рассматривать более общие анизотропные пространства (классы)  где l=(l1,...,ln) - положительный вектор (см. Вложения теоремы). Для каждого такого вектора lэффективно и в известной мере исчерпывающе определяется класс областей
где l=(l1,...,ln) - положительный вектор (см. Вложения теоремы). Для каждого такого вектора lэффективно и в известной мере исчерпывающе определяется класс областей  обладающих тем свойством, что если
обладающих тем свойством, что если  то любую функцию
то любую функцию  можно продолжить на
можно продолжить на  с сохранением класса. Точнее, можно определить на
с сохранением класса. Точнее, можно определить на  функцию
функцию  со свойствами
со свойствами

где сне зависит от f (см. [3]).
Благодаря этому свойству неравенства типа теорем вложения для функций  автоматически переносятся на функции
автоматически переносятся на функции 
Для векторов вида l=(l1,. . ., ln )области 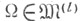 имеют липшицевы границы. Для них
имеют липшицевы границы. Для них 
Исследование пространств (классов) ведется на основе специальных интегральных представлений функций, принадлежащих этим классам. Первое такое представление получено (см. [1], [2]) для изотропного пространства
ведется на основе специальных интегральных представлений функций, принадлежащих этим классам. Первое такое представление получено (см. [1], [2]) для изотропного пространства  области
области  звездной относительно нек-рого шара. Дальнейшее развитие этого метода см., напр., в [3].
звездной относительно нек-рого шара. Дальнейшее развитие этого метода см., напр., в [3].
Классы Wlp и Wlp получили обобщение на случай дробных чисел пли векторов l=(l1,. . ., ln )с дробными компонентами lj.
Пространство  рассматривают и для отрицательных целых l. Элементами его являются, вообще говоря, обобщенные функции f, т. е. линейные функционалы
рассматривают и для отрицательных целых l. Элементами его являются, вообще говоря, обобщенные функции f, т. е. линейные функционалы  над финитными в
над финитными в  бесконечно дифференцируемыми функциями
бесконечно дифференцируемыми функциями 
По определению, обобщенная функция / принадлежит классу  при натуральном l = 1, 2, 3,. . ., вели конечна верхняя грань:
при натуральном l = 1, 2, 3,. . ., вели конечна верхняя грань:

распространенная на указанные функции j с нормой в метрике  не превышающей единицу (1/p+1/q=1). Можно еще сказать, что функции
не превышающей единицу (1/p+1/q=1). Можно еще сказать, что функции  l=1, 2,..., образуют пространство, сопряженное к банахову пространству
l=1, 2,..., образуют пространство, сопряженное к банахову пространству 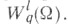
Лит.: [1] Соболев С. Л., лМатем. сб.

 функций f=f(x)=f(x1,...,xn), определенных на множестве
функций f=f(x)=f(x1,...,xn), определенных на множестве  (обычно открытом) и интегрируемых с р- йстепенью их модуля вместе со своими обобщенными производными до порядка lвключительно
(обычно открытом) и интегрируемых с р- йстепенью их модуля вместе со своими обобщенными производными до порядка lвключительно 

 определяется при помощи равенства
определяется при помощи равенства 

 и норма
и норма 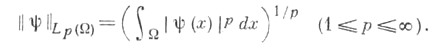
 эта норма равна существенному максимуму:
эта норма равна существенному максимуму: 
 имеет место на множестве меры нуль.
имеет место на множестве меры нуль.  определено и впервые применено в теории краевых задач матeматич. физики в [1], [2].
определено и впервые применено в теории краевых задач матeматич. физики в [1], [2].  рассматривается его линейное подпространство, обозначенное
рассматривается его линейное подпространство, обозначенное  и состоящее из функций, имеющих равномерно непрерывные на
и состоящее из функций, имеющих равномерно непрерывные на  частные производные l- гопорядка. Подпространство
частные производные l- гопорядка. Подпространство  имеет преимущества перед
имеет преимущества перед  однако оно не замкнуто в метрике
однако оно не замкнуто в метрике  и само по себе не является полным пространством, но для широкого класса областей (с липшициевой границей, см. ниже) при
и само по себе не является полным пространством, но для широкого класса областей (с липшициевой границей, см. ниже) при  пространство
пространство  плотно в
плотно в  т. е. для таких областей пространство
т. е. для таких областей пространство  кроме полноты, приобретает новое свойство, заключающееся в том, что каждая принадлежащая к нему функция может быть как угодно хорошо приближена в метрике
кроме полноты, приобретает новое свойство, заключающееся в том, что каждая принадлежащая к нему функция может быть как угодно хорошо приближена в метрике  функциями из
функциями из 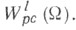
 удобно заменить на следующее выражение:
удобно заменить на следующее выражение: 

 где c1, с 2>0 не зависят от f). При р=2 норма (1') гильбертова, и это широко используется в приложениях.
где c1, с 2>0 не зависят от f). При р=2 норма (1') гильбертова, и это широко используется в приложениях.  наз. липшицевой, если, какова бы ни была точка
наз. липшицевой, если, какова бы ни была точка  найдется прямоугольная система координат
найдется прямоугольная система координат 
 с началом в этой точке и прямоугольник
с началом в этой точке и прямоугольник 
 описывается функцией
описывается функцией 

 (проекции
(проекции  на плоскость
на плоскость  условию Липшица
условию Липшица 

 и
и  Гладкие и многие кусочно гладкие границы охватываются понятием липшицевой границы. Для области с липшицевой границей норма (1) эквивалентна следующей:
Гладкие и многие кусочно гладкие границы охватываются понятием липшицевой границы. Для области с липшицевой границей норма (1) эквивалентна следующей: 

 где l=(l1,...,ln) - положительный вектор (см. Вложения теоремы). Для каждого такого вектора lэффективно и в известной мере исчерпывающе определяется класс областей
где l=(l1,...,ln) - положительный вектор (см. Вложения теоремы). Для каждого такого вектора lэффективно и в известной мере исчерпывающе определяется класс областей  обладающих тем свойством, что если
обладающих тем свойством, что если  то любую функцию
то любую функцию  можно продолжить на
можно продолжить на  с сохранением класса. Точнее, можно определить на
с сохранением класса. Точнее, можно определить на  функцию
функцию  со свойствами
со свойствами 
 автоматически переносятся на функции
автоматически переносятся на функции 
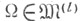 имеют липшицевы границы. Для них
имеют липшицевы границы. Для них 
 ведется на основе специальных интегральных представлений функций, принадлежащих этим классам. Первое такое представление получено (см. [1], [2]) для изотропного пространства
ведется на основе специальных интегральных представлений функций, принадлежащих этим классам. Первое такое представление получено (см. [1], [2]) для изотропного пространства  области
области  звездной относительно нек-рого шара. Дальнейшее развитие этого метода см., напр., в [3].
звездной относительно нек-рого шара. Дальнейшее развитие этого метода см., напр., в [3].  рассматривают и для отрицательных целых l. Элементами его являются, вообще говоря, обобщенные функции f, т. е. линейные функционалы
рассматривают и для отрицательных целых l. Элементами его являются, вообще говоря, обобщенные функции f, т. е. линейные функционалы  над финитными в
над финитными в  бесконечно дифференцируемыми функциями
бесконечно дифференцируемыми функциями 
 при натуральном l = 1, 2, 3,. . ., вели конечна верхняя грань:
при натуральном l = 1, 2, 3,. . ., вели конечна верхняя грань: 
 не превышающей единицу (1/p+1/q=1). Можно еще сказать, что функции
не превышающей единицу (1/p+1/q=1). Можно еще сказать, что функции  l=1, 2,..., образуют пространство, сопряженное к банахову пространству
l=1, 2,..., образуют пространство, сопряженное к банахову пространству