|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СМИРНОВА ОБЛАСТЬЗначение СМИРНОВА ОБЛАСТЬ в математической энциклопедии: область типа С, область типа S,- ограниченная односвязная область Gс жордановой спрямляемой границей на комплексной плоскости
Эти области введены В. И. Смирновым [1] в 1928 при исследовании полноты системы многочленов в Смирнова классе E2(G). Проблема существования несмирповских областей с жордановыми спрямляемыми границами была решена М. В. Келдышем и М. А. Лаврентьевым [2], давшими тонкую и сложную конструкцию таких областей и соответствующих отображающих функций j с дополнительным свойством: Лит.:[1] Смирнов В. И., лЖ. Ленингр. физ.-матем. об-ва
|
|
|
|
со свойством: существует такое однолистное конформное отображение 
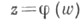круга | w|<1 на область G, что гармонич. функция 
при | w|< 1 продставима интегралом Пуассона по своим угловым граничным значениям 
почти для всех 
Основные граничные свойства аналитических функций в круге присущи и функциям, аналитическим в С. о., причем многие из таких свойств справедливы в С. о. и только в них. Примеры С. о. дают жордановы области, границы к-рых суть кривые Ляпунова или кусочно ляпуновские кривые с ненулевыми углами.