|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СМИРНОВА КЛАССЗначение СМИРНОВА КЛАСС в математической энциклопедии: Ep(G) - совокупность функций f(z), голоморфных в односвязной области
Это определение, предложенное М. В. Келдышем и М. А. Лаврентьевым [2], эквивалентно определению В. И. Смирнова [1], в к-ром вместо Г n(f) фигурируют кривые
По своим свойствам классы Е р (G)наиболее близки классам Н р в случае Смирнова областей G. Изучалось обобщение С. к. на случай произвольных областей Gс границами конечной длины по Хаусдорфу. См. также Граничные свойства аналитических функций. Лит.:[1] Смирнов В. И., лИзв. АН СССР. Отд. матем. и естеcтв. наук
|
|
|
|

 с жордановой спрямляемой границей Г и таких, что для каждой из этих функций существует последовательность замкнутых жордановых спрямляемых кривых
с жордановой спрямляемой границей Г и таких, что для каждой из этих функций существует последовательность замкнутых жордановых спрямляемых кривых 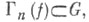 n=1,2,..., со свойствами: 1) Г n(f) при
n=1,2,..., со свойствами: 1) Г n(f) при  стремится к Г в том смысле, что если Gn(f) - ограниченная область с границей Г n(f), то
стремится к Г в том смысле, что если Gn(f) - ограниченная область с границей Г n(f), то 
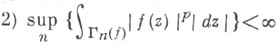 (р>0 задано).
(р>0 задано).  являющиеся образами соответствующих окружностей
являющиеся образами соответствующих окружностей  при нек-ром однолистном конформном отображении
при нек-ром однолистном конформном отображении  круга
круга  на область G, а супремум берется по
на область G, а супремум берется по 
 тогда и только тогда, когда
тогда и только тогда, когда 