"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СМЕШАННАЯ И КРАЕВАЯ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ
Значение СМЕШАННАЯ И КРАЕВАЯ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ в математической энциклопедии:
задачи отыскания решений уравнений и систем с частными производными гиперболич. типа, удовлетворяющих на границе области их задания (или ее части) определенным условиям (см. Краевые условия, Начальные условия).
Краевая задача для гиперболич. уравнений и систем, заданных в нек-рой области Dевклидова пространства 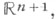 наз. смешанной, или начально-краевой, если искомое решение, наряду с краевыми условиями, должно удовлетворять и начальным или если носитель
наз. смешанной, или начально-краевой, если искомое решение, наряду с краевыми условиями, должно удовлетворять и начальным или если носитель 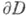 граничных данных состоит как из характеристических, так и нехарактеристических определенным образом ориентированных многообразий.
граничных данных состоит как из характеристических, так и нехарактеристических определенным образом ориентированных многообразий.
Для гиперболич. уравнений 2-го порядка носителем начальных данных при постановке смешанной задачи является пространственно ориентированная часть границы  На временным образом ориентированной части
На временным образом ориентированной части  как правило, задаются краевые условия такого же типа, как и для параболич. уравнений (см. Смешанная и краевая задачи для параболических уравнений и систем).
как правило, задаются краевые условия такого же типа, как и для параболич. уравнений (см. Смешанная и краевая задачи для параболических уравнений и систем).
Пусть  - область пространства
- область пространства  точек х= (х 1,х2, . . ., х п) с достаточно гладкой границей
точек х= (х 1,х2, . . ., х п) с достаточно гладкой границей  а
а


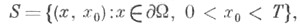
В области Dзадано линейное гиперболич. уравнение 2-го порядка

где подразумевается суммирование от 1 до ппо повторяющимся индексам i, j и форма  положительно определена.
положительно определена.
Основные смешанные задачи для уравнения (1) охватываются следующей постановкой: в области Dнайти решение и=и( х, x0) уравнения (1), удовлетворяющее на  начальным условиям
начальным условиям

а на S - одному из краевых условий



где N - конормаль относительного оператора 
Задачи (2), (3); (2), (4) и (2), (5) принято соответственно называть первой, второй и третьей смешанной задачей для уравнения (1).
Для уравнения (1) при довольно общих предположениях относительно его коэффициентов и границы  а также для заданных функций доказаны существование и единственность как регулярных, так и обобщенных решений всех трех смешанных задач, исследованы структурные и дифференциальные свойства этих решений в замкнутой области
а также для заданных функций доказаны существование и единственность как регулярных, так и обобщенных решений всех трех смешанных задач, исследованы структурные и дифференциальные свойства этих решений в замкнутой области 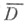 в зависимости от гладкости ее границы [8]. При п=1 решение сметанных задач выписывается в явном виде.
в зависимости от гладкости ее границы [8]. При п=1 решение сметанных задач выписывается в явном виде.
Смешанные задачи исследованы для широкого класса линейных и нелинейных гиперболич. уравнений и систем (см. Квазилинейные гиперболические уравнения и системы). Построена удовлетворительная теория смешанных задач для строго гиперболич. уравнений и систем вида

с начальными данными на (пространственно ориентированной) части границы области D, лежащей на плоскости х 0=0. Определенный успех достигнут и при изучении смешанных задач для гиперболич. уравнений и систем в случае, когда носители начальных или краевых условий представляют собой поверхности вырождения типа или порядка этих уравнений (см. Вырожденное уравнение с частными производными).
Наиболее существенные результаты получены для линейных уравнений 2-го порядка вида

с коэффициентами, удовлетворяющими условию

где  и
и  - нек-рые положительные постоянные, и особенно для уравнений вида
- нек-рые положительные постоянные, и особенно для уравнений вида

К смешанным задачам с внутренними или внешними краевыми условиями (см. Внешняя и внутренняя краевые задачи )редуцируются математич. модели многих процессов теории рассеяния волн на препятствиях. Напр., к условию излучения Зоммерфельда (см. Излучения условия )приводит задача отыскания решения иволнового уравнения

для всех точек  лежащих вне ограниченной области
лежащих вне ограниченной области  если известно, что производная ипо направлению внешней нормали и
если известно, что производная ипо направлению внешней нормали и  обращается в нуль для любого момента времени
обращается в нуль для любого момента времени  а начальные условия соответствуют плоской волне, идущей из бесконечности в направлении оси х 1.
а начальные условия соответствуют плоской волне, идущей из бесконечности в направлении оси х 1.
Основными краевыми задачами для гиперболич. уравнений и систем являются Гурса, Дарбу - Пикара и их многомерные аналоги (см. Гурса задача, Коши характеристическая задача, а также [1]).
Задачи Гурса, Дарбу - Пикара и их различные обобщения хорошо исследованы для гиперболич. уравнений и систем 2-го порядка с расщепленными главными частями вида

где а, bи с - заданные действительные  -матрицы, f- заданный, а и - искомый m-мерные векторы. Существенные результаты получены и для довольно широкого класса гиперболич. систем уравнений 2-го порядка с, нерасщепленными главными частями при отсутствии параболич. вырождения. Обнаружен факт неединственности решения характеристич. задачи Гурса
-матрицы, f- заданный, а и - искомый m-мерные векторы. Существенные результаты получены и для довольно широкого класса гиперболич. систем уравнений 2-го порядка с, нерасщепленными главными частями при отсутствии параболич. вырождения. Обнаружен факт неединственности решения характеристич. задачи Гурса

для гиперболич. системы

с двумя независимыми переменными х, у и найден эффект влияния младших членов на корректность этой задачи [3]. Достаточно полно изучен вопрос влияния характера параболич. вырождений на корректность как локальных, так и нелокальных краевых задач для вырождающихся гиперболич. уравнений и систем [3]. В частности, исследованы основные (локальные) краевые задачи для линейных вырождающихся гиперболич. уравнений вида
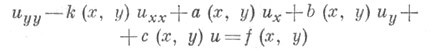
в ограниченных областях с произвольной кусочно гладкой границей, установлен факт влияния порядка нехарактеристич. вырождения на корректность задачи Дарбу и неравноправия характеристик как носителей краевых условий [10].
В связи с проблемой поиска многомерных аналогов задач Дарбу и Трикоми (см. Смешанного типа уравнения )начались интенсивные исследования нелокальных краевых задач и особенно задачи со смещением (см. [9]) для гиперболич. уравнений, когда на характеристич. частях границы задано условие, поточечно связывающее значения искомого решения или его (дробных) производных или интегралов определенного порядка.
Многие краевые задачи со смещением, изучаемые с большой полнотой и общностью в случае уравнения (1), охватываются следующей постановкой. В области, ограниченной характеристиками


и отрезком I : 0<x<1 прямой у =0,найти (достаточно гладкое) решение и(x, у )уравнения (1), удовлетворяющее на Iлокальному условию

а на  - нелокальному условию
- нелокальному условию

Здесь А i, В i, а i - заданные функции,  -оператор дробного интегро-дифференцирования порядка
-оператор дробного интегро-дифференцирования порядка  задаваемый формулой
задаваемый формулой

если  и
и

если  где Г (z) - гамма-функция,
где Г (z) - гамма-функция, - целая часть
- целая часть 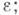
 - точка пересечения характеристики, выходящей из точки
- точка пересечения характеристики, выходящей из точки  с характеристикой Г j уравнения (1):
с характеристикой Г j уравнения (1):
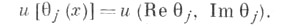
Подробно изучены краевые задачи со смещением для уравнения вида (1), к-рые в характеристич. координатах  и
и  редуцируются к уравнению Эйлера - Дарбу - Пуассона
редуцируются к уравнению Эйлера - Дарбу - Пуассона

Частным случаем задачи (7) - (8) является задача Дарбу, к-рая состоит в отыскании (достаточно гладкого) решения .( х, у )уравнения (6), удовлетворяющего (локальным) краевым условиям

или

Условие m<2 или  (условие Геллерстедта), является существенным для корректности задачи Дарбу (см. [3], [10]).
(условие Геллерстедта), является существенным для корректности задачи Дарбу (см. [3], [10]).
Качественно новым многомерным аналогом задачи Дарбу является задача Бицадзе, к-рая в случае волнового уравнения  ставится следующим образом (см. [1]). В конечной области
ставится следующим образом (см. [1]). В конечной области  ограниченной частью S0 плоскости х n=0 и двумяхарактеристич. поверхностями
ограниченной частью S0 плоскости х n=0 и двумяхарактеристич. поверхностями

и

найти решение уравнения, удовлетворяющее условиям  или
или 
Изучены и другие многомерные аналоги как задачи Дарбу, так и нелокальных краевых задач (типа [2], [3]) для гиперболич. уравнений в специальных областях, нехарактеристич. часть границы к-рых, как правило, представляет собой пространственно ориентированную поверхность. Наиболее полные результаты получены в случае уравнения Эйлера - Дарбу - Пуассона 
Для уравнения вида

весьма полно исследована нелокальная задача в следующей постановке. В области {( х, у) :0<x<h, 0<y<Т}найти (достаточно гладкое) решение и( х, у )уравнения (9), если для всех  известно, что
известно, что

или

где x0, x1, . . ., xq - заданные точки из сегмента [0, h].
В теорию краевых задач вносится новый аспект при переходе к гиперболич. уравнениям 3-го порядка вида

к-рые лежат в основе математич. моделей многих процессов и явлений теории тепломассообмена в пористых средах. Построена содержательная теория как локальных, так и нелокальных линейных краевых задач для гиперболич. уравнений вида (10), в частности создан аналог метода Римана.
Для линейных симметрических гиперболич. систем 1-го порядка (см. Линейное гиперболическое уравнение и система) в рамках теории систем уравнений 1-го порядка изучены краевые задачи с допустимыми (см. [6]) краевыми условиями на 
Задача Дирихле, вообще говоря, не является корректной для гиперболич. уравнений и систем в произвольных областях. Методами энергетич. оценок и интегральных уравнений установлена корректность этой задачи для широкого класса гиперболич. уравнений 2-го порядка в специальных цилиндрич. областях.
Лит.:[1] Бицадзе А. В., Некоторые классы уравнений в частных производных, М., 1981; [2] Владимиров В. С., Уравнения математической физики, 4 изд., М., 1981; [3] Gе11еrstedt S., лArk. mat., astr., fys.

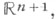 наз. смешанной, или начально-краевой, если искомое решение, наряду с краевыми условиями, должно удовлетворять и начальным или если носитель
наз. смешанной, или начально-краевой, если искомое решение, наряду с краевыми условиями, должно удовлетворять и начальным или если носитель 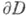 граничных данных состоит как из характеристических, так и нехарактеристических определенным образом ориентированных многообразий.
граничных данных состоит как из характеристических, так и нехарактеристических определенным образом ориентированных многообразий.  На временным образом ориентированной части
На временным образом ориентированной части  как правило, задаются краевые условия такого же типа, как и для параболич. уравнений (см. Смешанная и краевая задачи для параболических уравнений и систем).
как правило, задаются краевые условия такого же типа, как и для параболич. уравнений (см. Смешанная и краевая задачи для параболических уравнений и систем).  - область пространства
- область пространства  точек х= (х 1,х2, . . ., х п) с достаточно гладкой границей
точек х= (х 1,х2, . . ., х п) с достаточно гладкой границей  а
а 

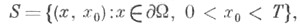

 положительно определена.
положительно определена.  начальным условиям
начальным условиям 




 а также для заданных функций доказаны существование и единственность как регулярных, так и обобщенных решений всех трех смешанных задач, исследованы структурные и дифференциальные свойства этих решений в замкнутой области
а также для заданных функций доказаны существование и единственность как регулярных, так и обобщенных решений всех трех смешанных задач, исследованы структурные и дифференциальные свойства этих решений в замкнутой области 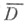 в зависимости от гладкости ее границы [8]. При п=1 решение сметанных задач выписывается в явном виде.
в зависимости от гладкости ее границы [8]. При п=1 решение сметанных задач выписывается в явном виде. 


 и
и  - нек-рые положительные постоянные, и особенно для уравнений вида
- нек-рые положительные постоянные, и особенно для уравнений вида 

 лежащих вне ограниченной области
лежащих вне ограниченной области  если известно, что производная ипо направлению внешней нормали и
если известно, что производная ипо направлению внешней нормали и  обращается в нуль для любого момента времени
обращается в нуль для любого момента времени  а начальные условия соответствуют плоской волне, идущей из бесконечности в направлении оси х 1.
а начальные условия соответствуют плоской волне, идущей из бесконечности в направлении оси х 1. 
 -матрицы, f- заданный, а и - искомый m-мерные векторы. Существенные результаты получены и для довольно широкого класса гиперболич. систем уравнений 2-го порядка с, нерасщепленными главными частями при отсутствии параболич. вырождения. Обнаружен факт неединственности решения характеристич. задачи Гурса
-матрицы, f- заданный, а и - искомый m-мерные векторы. Существенные результаты получены и для довольно широкого класса гиперболич. систем уравнений 2-го порядка с, нерасщепленными главными частями при отсутствии параболич. вырождения. Обнаружен факт неединственности решения характеристич. задачи Гурса 

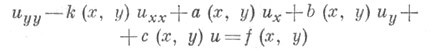



 - нелокальному условию
- нелокальному условию 
 -оператор дробного интегро-дифференцирования порядка
-оператор дробного интегро-дифференцирования порядка  задаваемый формулой
задаваемый формулой 
 и
и 
 где Г (z) - гамма-функция,
где Г (z) - гамма-функция, - целая часть
- целая часть 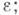
 - точка пересечения характеристики, выходящей из точки
- точка пересечения характеристики, выходящей из точки  с характеристикой Г j уравнения (1):
с характеристикой Г j уравнения (1): 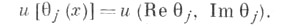
 и
и  редуцируются к уравнению Эйлера - Дарбу - Пуассона
редуцируются к уравнению Эйлера - Дарбу - Пуассона 


 (условие Геллерстедта), является существенным для корректности задачи Дарбу (см. [3], [10]).
(условие Геллерстедта), является существенным для корректности задачи Дарбу (см. [3], [10]).  ставится следующим образом (см. [1]). В конечной области
ставится следующим образом (см. [1]). В конечной области  ограниченной частью S0 плоскости х n=0 и двумяхарактеристич. поверхностями
ограниченной частью S0 плоскости х n=0 и двумяхарактеристич. поверхностями 

 или
или 


 известно, что
известно, что 


