"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЛУЧАЙНЫЙ ПРОЦЕСС
Значение СЛУЧАЙНЫЙ ПРОЦЕСС в математической энциклопедии:
стохастический процесс, вероятностный процесс, случайная функция времени, - процесс (т. е. изменение во времени состояния нек-рой системы), течение к-рого зависит от случая и для к-рого определена вероятность того или иного его течения. Типичным примером С. п. может служить броуновского движения процесс. Другими практически важными примерами С. п. являются: процесс протекания тока в электрич. цепи, сопровождающийся неупорядоченными флуктуациями силы тока и напряжения (шумами); распространение радиоволн при наличии случайных замираний радиосигналов (федингов), создаваемых метеорологическими или иными помехами, и турбулентные течения жидкости или газа. К числу С. н. могут быть причислены и многие производственные процессы, сопровождающиеся случайными флуктуациями, а также процессы, встречающиеся в геофизике (напр., вариации земного магнитного поля, морское волнение, или микросейсмы,- высокочастотные беспорядочные колебания уровня земной поверхности), биофизике (напр., изменения биоэлектрич. потенциалов мозга, регистрируемые на электроэнцефалограмме) и экономике.
Математич. теория С. п. рассматривает мгновенное состояние системы, о к-рой идет речь, как точку нек-рого фазового пространства (пространства состояний) R;при этом С. п. представляется функцией X(t)времени tсо значениями из R. Обычно считается, что R - векторное пространство, причем наиболее изученным (и в то же время наиболее важным с точки зрения приложений) является еще более узкий случай, когда точки Rзадаются одним или несколькими числовыми параметрами (обобщенными координатами системы), т. е. С. п. можно рассматривать или просто как числовую функцию времени X(t), в зависимости от случая принимающую различные значения, т. е. допускающую различные реализации х(t) (одномерный С. п.), или как подобную же векторную функцию X(t}= ={X1(t), . . ., Х k(t)}(многомерный, или векторный, С. п.). Изучение многомерных С. п. можно свести к изучению одномерных С. п. с помощью перехода от X(t)к вспомогательному процессу
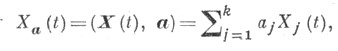
где а= (a1.. . ., а k) - произвольный k-мерный вектор; поэтому центральное место в теории С. п. занимает исследование одномерных процессов X(t). Параметр tобычно принимает произвольные действительные значения или же значения из какого-то интервала действительной оси R1 (когда хотят подчеркнуть это обстоятельство, то говорят о С. п. с непрерывным временем), но он может пробегать и только целочисленные значения - тогда . наз. С. п. с дискретным временем (или случайной последовательностью, или временным рядом).
Задание распределения вероятностей в бесконечномерном пространстве всевозможных вариантов протекания С. п. X(t)(т. е. в пространстве реализаций x(t))не укладывается в рамки классич. методов теории вероятностей и требует привлечения специального математич. аппарата. Исключением являются лишь частные классы С. п., вероятностный характер к-рых полностью определяется зависимостью функции X(t)= =Х (t; Y )от нек-рого конечномерного случайного вектора Y= (Y1, . ..,Yk), т. к. в данном случае вероятность того или иного протекания X(t)зависит только от конечномерного распределения вероятностей вектора Y. Практически важным примером С. п. такого рода может служить случайное гармонич. колебание вида
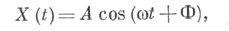
где 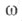 - фиксированное число, Аи Ф - независимые случайные величины, часто используемое при исследовании амплитудно-фазовой модуляции в радиотехнике. Широкий класс распределений вероятностей для С. н. может быть охарактеризован бесконечной совокупностью согласованных друг с другом конечномерных распределений вероятностей случайных векторов {X(t1), X(t2), . . ., X(tn)},отвечающих всевозможным конечным подмножествам (t1, t2, . . ., tn) значений аргумента t(см. Случайная функция). Однако задание всех этих распределений все же недостаточно для определения вероятностей событий, зависящих от значений X(t)на бесконечном множестве значений t, т. е. не определяет однозначно С. п. X(t).
- фиксированное число, Аи Ф - независимые случайные величины, часто используемое при исследовании амплитудно-фазовой модуляции в радиотехнике. Широкий класс распределений вероятностей для С. н. может быть охарактеризован бесконечной совокупностью согласованных друг с другом конечномерных распределений вероятностей случайных векторов {X(t1), X(t2), . . ., X(tn)},отвечающих всевозможным конечным подмножествам (t1, t2, . . ., tn) значений аргумента t(см. Случайная функция). Однако задание всех этих распределений все же недостаточно для определения вероятностей событий, зависящих от значений X(t)на бесконечном множестве значений t, т. е. не определяет однозначно С. п. X(t).
Пример. Пусть 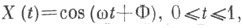 - гармонич. колебание со случайной фазой Ф, Z - случайная величина, равномерно распределенная на отрезке [0, 1], а С. п. Xl(t),
- гармонич. колебание со случайной фазой Ф, Z - случайная величина, равномерно распределенная на отрезке [0, 1], а С. п. Xl(t), 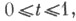 задается равенствами X1(t)= X(t) при
задается равенствами X1(t)= X(t) при 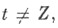 Х 1(t) = X(t)+3 при t= Z.
Х 1(t) = X(t)+3 при t= Z.
Так как P{Z=tl, или Z=t2, . . ., или Z=tn}=0для любой фиксированной конечной группы точек (t1, t2, . . ., tn), то все конечномерные распределения С. п. X(t) и X1(t)являются одинаковыми. В то же время процессы X(t)и Х 1(t)различаются между собой: в частности, все реализации процесса X(t)непрерывны (имеют форму синусоиды), в то время как все реализации Х 1(t) имеют точку разрыва; все реализации X(t)не превосходят числа 1, но ни одна реализация Х 1(t)этим свойством не обладает. Отсюда следует, что заданной системе конечномерных распределений вероятностей могут отвечать различные модификации С. п. и по одним только конечномерным распределениям нельзя вычислить ни вероятность того, что реализация С. п. будет непрерывной, ни того, что она будет ограничена нек-рой фиксированной постоянной.
Задание совокупности конечномерных распределений вероятностей часто позволяет, однако, выяснить, существует ли хоть один С. п. X(t), имеющий эти конечномерные распределения, и такой, что его реализации являются непрерывными (или, напр., дифференцируемыми, или нигде не превосходящими заданной постоянной В)функциями с вероятностью 1, или же таких С. п. X(t)вообще не существует. Типичным примером общего условия, гарантирующего существование С. п. X(t) с непрерывными с вероятностью 1 реализациями, имеющего заданные конечномерные распределения, является условие Колмогорова: если конечномерные распределения вероятностей С. п. X(t), определенного на интервале [ а, b], таковы, что при нек-рых 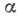 >0, b>0 и
>0, b>0 и 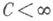 для всех достаточно малых hвыполняется неравенство
для всех достаточно малых hвыполняется неравенство
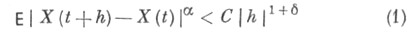
(очевидно, накладывающее ограничения лишь на двумерные распределения X(t)), то С. п. X(t)имеет модификацию с непрерывными с вероятностью 1 реализациями (см., напр., [1] - [6]). В частном случае гауссовского процесса X(t)условие (1) может быть заменено более слабым условием:
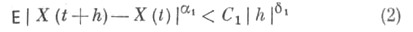
для нек-рых 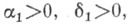 С 1>0; при
С 1>0; при 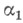 =2,
=2, 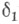 =1 условие (2) выполняется, напр., для винероеского процесса и Орнштейна - Уленбека процесса. В случаях когда при заданных конечномерных распределениях вероятностей существует модификация С. п. X(t)такая, что ее реализации непрерывны (или, напр., дифференцируемы, или ограничены постоянной В) с вероятностью 1, все другие модификации этого же процесса обычно можно исключить из рассмотрения, потребовав, чтобы С. п. X(t)удовлетворял нек-рому очень общему условию регулярности, к-рое в прикладных задачах практически всегда можно считать выполняющимся (см. Сепарабелъный процесс).
=1 условие (2) выполняется, напр., для винероеского процесса и Орнштейна - Уленбека процесса. В случаях когда при заданных конечномерных распределениях вероятностей существует модификация С. п. X(t)такая, что ее реализации непрерывны (или, напр., дифференцируемы, или ограничены постоянной В) с вероятностью 1, все другие модификации этого же процесса обычно можно исключить из рассмотрения, потребовав, чтобы С. п. X(t)удовлетворял нек-рому очень общему условию регулярности, к-рое в прикладных задачах практически всегда можно считать выполняющимся (см. Сепарабелъный процесс).
Вместо того чтобы задавать бесконечную совокупность конечномерных распределений вероятностей С. п. X(t), можно также определить С. п., указав значение соответствующего характеристического функционала
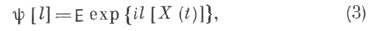
где l[X(t)] пробегает достаточно широкий класс линейных функционалов, зависящих от X(t). Если X(t), 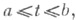 -непрерывный по вероятности С. п. (т. е.
-непрерывный по вероятности С. п. (т. е. 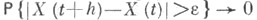 при
при 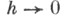 для любого
для любого 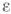 >0), a g(t) - функция ограниченной вариации на [ а, b]. то
>0), a g(t) - функция ограниченной вариации на [ а, b]. то
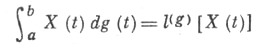
будет случайной величиной; при этом можно считать, что 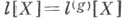 в формуле (3) (причем
в формуле (3) (причем 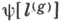 здесь удобно обозначить символом
здесь удобно обозначить символом 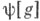 ). Во многих случаях можно также еще сузить класс рассматриваемых линейных функционалов l[Х],ограничившись лить функционалами вида
). Во многих случаях можно также еще сузить класс рассматриваемых линейных функционалов l[Х],ограничившись лить функционалами вида
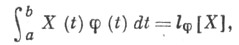
где 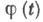 - финитная бесконечно дифференцируемая функция t(интервал [ а, b]при этом может быть и бесконечным). Значения
- финитная бесконечно дифференцируемая функция t(интервал [ а, b]при этом может быть и бесконечным). Значения 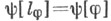 при широких условиях регулярности однозначно определяют все конечномерные распределения вероятностей С. п. X(t), так как .
при широких условиях регулярности однозначно определяют все конечномерные распределения вероятностей С. п. X(t), так как .
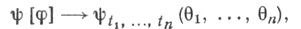
где 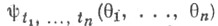 - характеристич. функция случайного вектора {X(t1), . . ., X(tn)}, при
- характеристич. функция случайного вектора {X(t1), . . ., X(tn)}, при 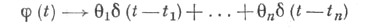
(здесь 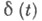 есть
есть 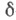 -функция Дирака, а сходимость понимается в смысле сходимости обобщенных функций). Если же при таком предельном переходе функционал
-функция Дирака, а сходимость понимается в смысле сходимости обобщенных функций). Если же при таком предельном переходе функционал 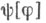 не стремится к конечному пределу, то это означает, что для С. п. Xне существует конечных значений в фиксированной точке, а имеют смысл лишь сглаженные значения
не стремится к конечному пределу, то это означает, что для С. п. Xне существует конечных значений в фиксированной точке, а имеют смысл лишь сглаженные значения 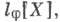 т. е. что характеристич. функционал
т. е. что характеристич. функционал 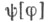 задает не обыкновенный (лклассический
задает не обыкновенный (лклассический

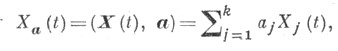
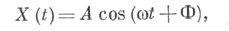
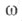 - фиксированное число, Аи Ф - независимые случайные величины, часто используемое при исследовании амплитудно-фазовой модуляции в радиотехнике. Широкий класс распределений вероятностей для С. н. может быть охарактеризован бесконечной совокупностью согласованных друг с другом конечномерных распределений вероятностей случайных векторов {X(t1), X(t2), . . ., X(tn)},отвечающих всевозможным конечным подмножествам (t1, t2, . . ., tn) значений аргумента t(см. Случайная функция). Однако задание всех этих распределений все же недостаточно для определения вероятностей событий, зависящих от значений X(t)на бесконечном множестве значений t, т. е. не определяет однозначно С. п. X(t).
- фиксированное число, Аи Ф - независимые случайные величины, часто используемое при исследовании амплитудно-фазовой модуляции в радиотехнике. Широкий класс распределений вероятностей для С. н. может быть охарактеризован бесконечной совокупностью согласованных друг с другом конечномерных распределений вероятностей случайных векторов {X(t1), X(t2), . . ., X(tn)},отвечающих всевозможным конечным подмножествам (t1, t2, . . ., tn) значений аргумента t(см. Случайная функция). Однако задание всех этих распределений все же недостаточно для определения вероятностей событий, зависящих от значений X(t)на бесконечном множестве значений t, т. е. не определяет однозначно С. п. X(t). 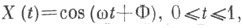 - гармонич. колебание со случайной фазой Ф, Z - случайная величина, равномерно распределенная на отрезке [0, 1], а С. п. Xl(t),
- гармонич. колебание со случайной фазой Ф, Z - случайная величина, равномерно распределенная на отрезке [0, 1], а С. п. Xl(t), 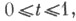 задается равенствами X1(t)= X(t) при
задается равенствами X1(t)= X(t) при 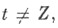 Х 1(t) = X(t)+3 при t= Z.
Х 1(t) = X(t)+3 при t= Z. 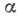 >0, b>0 и
>0, b>0 и 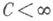 для всех достаточно малых hвыполняется неравенство
для всех достаточно малых hвыполняется неравенство 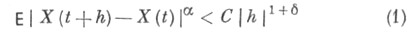
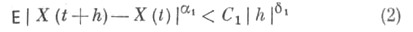
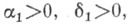 С 1>0; при
С 1>0; при 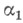 =2,
=2, 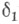 =1 условие (2) выполняется, напр., для винероеского процесса и Орнштейна - Уленбека процесса. В случаях когда при заданных конечномерных распределениях вероятностей существует модификация С. п. X(t)такая, что ее реализации непрерывны (или, напр., дифференцируемы, или ограничены постоянной В) с вероятностью 1, все другие модификации этого же процесса обычно можно исключить из рассмотрения, потребовав, чтобы С. п. X(t)удовлетворял нек-рому очень общему условию регулярности, к-рое в прикладных задачах практически всегда можно считать выполняющимся (см. Сепарабелъный процесс).
=1 условие (2) выполняется, напр., для винероеского процесса и Орнштейна - Уленбека процесса. В случаях когда при заданных конечномерных распределениях вероятностей существует модификация С. п. X(t)такая, что ее реализации непрерывны (или, напр., дифференцируемы, или ограничены постоянной В) с вероятностью 1, все другие модификации этого же процесса обычно можно исключить из рассмотрения, потребовав, чтобы С. п. X(t)удовлетворял нек-рому очень общему условию регулярности, к-рое в прикладных задачах практически всегда можно считать выполняющимся (см. Сепарабелъный процесс). 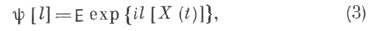
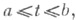 -непрерывный по вероятности С. п. (т. е.
-непрерывный по вероятности С. п. (т. е. 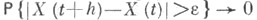 при
при 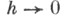 для любого
для любого 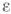 >0), a g(t) - функция ограниченной вариации на [ а, b]. то
>0), a g(t) - функция ограниченной вариации на [ а, b]. то 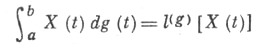
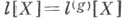 в формуле (3) (причем
в формуле (3) (причем 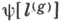 здесь удобно обозначить символом
здесь удобно обозначить символом 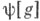 ). Во многих случаях можно также еще сузить класс рассматриваемых линейных функционалов l[Х],ограничившись лить функционалами вида
). Во многих случаях можно также еще сузить класс рассматриваемых линейных функционалов l[Х],ограничившись лить функционалами вида 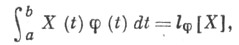
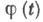 - финитная бесконечно дифференцируемая функция t(интервал [ а, b]при этом может быть и бесконечным). Значения
- финитная бесконечно дифференцируемая функция t(интервал [ а, b]при этом может быть и бесконечным). Значения 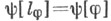 при широких условиях регулярности однозначно определяют все конечномерные распределения вероятностей С. п. X(t), так как .
при широких условиях регулярности однозначно определяют все конечномерные распределения вероятностей С. п. X(t), так как . 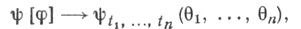
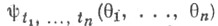 - характеристич. функция случайного вектора {X(t1), . . ., X(tn)}, при
- характеристич. функция случайного вектора {X(t1), . . ., X(tn)}, при 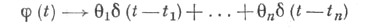
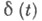 есть
есть 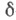 -функция Дирака, а сходимость понимается в смысле сходимости обобщенных функций). Если же при таком предельном переходе функционал
-функция Дирака, а сходимость понимается в смысле сходимости обобщенных функций). Если же при таком предельном переходе функционал 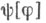 не стремится к конечному пределу, то это означает, что для С. п. Xне существует конечных значений в фиксированной точке, а имеют смысл лишь сглаженные значения
не стремится к конечному пределу, то это означает, что для С. п. Xне существует конечных значений в фиксированной точке, а имеют смысл лишь сглаженные значения 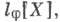 т. е. что характеристич. функционал
т. е. что характеристич. функционал 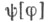 задает не обыкновенный (лклассический
задает не обыкновенный (лклассический