"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЛУЧАЙНЫЕ РАЗМЕЩЕНИЯ
Значение СЛУЧАЙНЫЕ РАЗМЕЩЕНИЯ в математической энциклопедии:
вероятностная схема, в к-рой пчастиц случайно размещаются в Nячейках. В наиболее простой схеме равновероятных размещений каждая из пчастиц независимо от других частиц может попасть в любую фиксированную ячейку с вероятностью 1/N. Пусть  - число ячеек, в к-рых после такого размещения оказалось ровно rчастиц и пусть
- число ячеек, в к-рых после такого размещения оказалось ровно rчастиц и пусть  Производящая функция
Производящая функция

имеет следующий вид:

Производящая функция (1) позволяет вычислять моменты  и изучать асимптотич. свойства распределений
и изучать асимптотич. свойства распределений  при n,
при n,  Эти асимптотич. свойства в значительной степени определяются поведением параметра
Эти асимптотич. свойства в значительной степени определяются поведением параметра 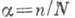 - среднего числа частиц на одну ячейку. Если п,
- среднего числа частиц на одну ячейку. Если п,  и
и 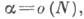 то при фиксированных rи t
то при фиксированных rи t

где 

 - символ Кронекера. Можно выделить пять различных типов областей, в к-рых асимптотич. поведение
- символ Кронекера. Можно выделить пять различных типов областей, в к-рых асимптотич. поведение  различны.
различны.
Центральной областью наз. такая область изменения п,  для к-рой
для к-рой  Область п,
Область п,  в к-рой
в к-рой

наз. правой r-областью. Правой промежуточной областью наз. область изменения п,  в к-рой
в к-рой 
Для  левой r-областью наз. область изменений п,
левой r-областью наз. область изменений п,  для к-рой
для к-рой 
Левой промежуточной r-областью наз. область, в к-рой 
Левые и левые промежуточные r-области для r=0,1 считают совпадающими с соответствующими 2-областями.
В равновероятной схеме размещения в правой r-области 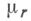 имеет асимптотически пуассоновское распределение. В левой r-области
имеет асимптотически пуассоновское распределение. В левой r-области  имеет при
имеет при  также в пределе пуассоновское распределение; при r=0 и r=1 предельные пуассоновские распределения имеют
также в пределе пуассоновское распределение; при r=0 и r=1 предельные пуассоновские распределения имеют  и
и  В левых и правых промежуточных r-областях
В левых и правых промежуточных r-областях  имеют асимптотически нормальное распределение. В центральной области доказана многомерная нормальная теорема для
имеют асимптотически нормальное распределение. В центральной области доказана многомерная нормальная теорема для  параметры предельного нормального распределения определяются асимптотич. формулами (2) (см. [1]).
параметры предельного нормального распределения определяются асимптотич. формулами (2) (см. [1]).
Размещение, в к-ром пчастиц независимо друг от друга распределяются по N ячейкам и вероятность каждой из частиц попасть в j-ю ячейку равна  1, наз. полиномиальным. Для полиномиального размещения также можно ввести центральную, правые и левые области изменений п, N и al, для к-рых доказаны предельные нормальные и пуассоновские теоремы (см. [1], [3]). Пользуясь этими теоремами, можно рассчитать мощность пустых ящиков критерия. Пусть имеются независимые случайные величины
1, наз. полиномиальным. Для полиномиального размещения также можно ввести центральную, правые и левые области изменений п, N и al, для к-рых доказаны предельные нормальные и пуассоновские теоремы (см. [1], [3]). Пользуясь этими теоремами, можно рассчитать мощность пустых ящиков критерия. Пусть имеются независимые случайные величины  . . .,
. . ., каждая из к-рых имеет непрерывную функцию распределения F(х)(гипотеза H0). Конкурирующая гипотеза Н 1 соответствует другой функции распределения F1(x). Точки
каждая из к-рых имеет непрерывную функцию распределения F(х)(гипотеза H0). Конкурирующая гипотеза Н 1 соответствует другой функции распределения F1(x). Точки  выбирают так, чтобы F(zk)-F(zk-1)=l/N, k=1, . . .,N. Критерий пустых ящиков строится на основе статистики
выбирают так, чтобы F(zk)-F(zk-1)=l/N, k=1, . . .,N. Критерий пустых ящиков строится на основе статистики  равной числу полуинтервалов
равной числу полуинтервалов  в к-рые не попало ни одного значения
в к-рые не попало ни одного значения  Критерии пустых ящиков определяется критич. множеством
Критерии пустых ящиков определяется критич. множеством  >С, при к-ром гипотеза H0 отвергается. Поскольку
>С, при к-ром гипотеза H0 отвергается. Поскольку  имеет при основной гипотезе H0 распределение, определяемое равномерным размещением, а при конкурирующей гипотезе Н 1- распределение, определяемое полиномиальным размещением, то можно воспользоваться предельными теоремами для
имеет при основной гипотезе H0 распределение, определяемое равномерным размещением, а при конкурирующей гипотезе Н 1- распределение, определяемое полиномиальным размещением, то можно воспользоваться предельными теоремами для  при расчете мощности
при расчете мощности  этого критерия (см. [2]).
этого критерия (см. [2]).
В схеме размещения частиц комплектами предполагается, что частицы размещаются в Nячейках комплектами по тчастиц, причем частицы одного комплекта могут располагаться в ячейках только по одной, а расположения комплектов независимы. Если все  расположения комплектов равновероятны, а число комплектов
расположения комплектов равновероятны, а число комплектов  то при ограниченных или слабо растущих тсохраняются свойства асимптотич. нормальности и предельной пуассоновости случайных величин
то при ограниченных или слабо растущих тсохраняются свойства асимптотич. нормальности и предельной пуассоновости случайных величин 
Возможны различные обобщения схем размещения (см. [1]), связанные с целым рядом комбинаторных задач теории вероятностей (случайные подстановки, отображения, деревья и т. п.).
Лит.:[l] Колчин В. Ф., Севастьянов Б. Л., Чистяков В. П., Случайные размещения, М., 1976; [2] Севастьянов Б. А., лТруды ин-та прикладной математики Тбилисского ун-та

 - число ячеек, в к-рых после такого размещения оказалось ровно rчастиц и пусть
- число ячеек, в к-рых после такого размещения оказалось ровно rчастиц и пусть  Производящая функция
Производящая функция 

 и изучать асимптотич. свойства распределений
и изучать асимптотич. свойства распределений  при n,
при n,  Эти асимптотич. свойства в значительной степени определяются поведением параметра
Эти асимптотич. свойства в значительной степени определяются поведением параметра 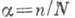 - среднего числа частиц на одну ячейку. Если п,
- среднего числа частиц на одну ячейку. Если п,  и
и 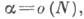 то при фиксированных rи t
то при фиксированных rи t 


 - символ Кронекера. Можно выделить пять различных типов областей, в к-рых асимптотич. поведение
- символ Кронекера. Можно выделить пять различных типов областей, в к-рых асимптотич. поведение  различны.
различны.  для к-рой
для к-рой  Область п,
Область п,  в к-рой
в к-рой 
 в к-рой
в к-рой 
 левой r-областью наз. область изменений п,
левой r-областью наз. область изменений п,  для к-рой
для к-рой 

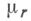 имеет асимптотически пуассоновское распределение. В левой r-области
имеет асимптотически пуассоновское распределение. В левой r-области  имеет при
имеет при  также в пределе пуассоновское распределение; при r=0 и r=1 предельные пуассоновские распределения имеют
также в пределе пуассоновское распределение; при r=0 и r=1 предельные пуассоновские распределения имеют  и
и  В левых и правых промежуточных r-областях
В левых и правых промежуточных r-областях  имеют асимптотически нормальное распределение. В центральной области доказана многомерная нормальная теорема для
имеют асимптотически нормальное распределение. В центральной области доказана многомерная нормальная теорема для  параметры предельного нормального распределения определяются асимптотич. формулами (2) (см. [1]).
параметры предельного нормального распределения определяются асимптотич. формулами (2) (см. [1]).  1, наз. полиномиальным. Для полиномиального размещения также можно ввести центральную, правые и левые области изменений п, N и al, для к-рых доказаны предельные нормальные и пуассоновские теоремы (см. [1], [3]). Пользуясь этими теоремами, можно рассчитать мощность пустых ящиков критерия. Пусть имеются независимые случайные величины
1, наз. полиномиальным. Для полиномиального размещения также можно ввести центральную, правые и левые области изменений п, N и al, для к-рых доказаны предельные нормальные и пуассоновские теоремы (см. [1], [3]). Пользуясь этими теоремами, можно рассчитать мощность пустых ящиков критерия. Пусть имеются независимые случайные величины  . . .,
. . ., каждая из к-рых имеет непрерывную функцию распределения F(х)(гипотеза H0). Конкурирующая гипотеза Н 1 соответствует другой функции распределения F1(x). Точки
каждая из к-рых имеет непрерывную функцию распределения F(х)(гипотеза H0). Конкурирующая гипотеза Н 1 соответствует другой функции распределения F1(x). Точки  выбирают так, чтобы F(zk)-F(zk-1)=l/N, k=1, . . .,N. Критерий пустых ящиков строится на основе статистики
выбирают так, чтобы F(zk)-F(zk-1)=l/N, k=1, . . .,N. Критерий пустых ящиков строится на основе статистики  равной числу полуинтервалов
равной числу полуинтервалов  в к-рые не попало ни одного значения
в к-рые не попало ни одного значения  Критерии пустых ящиков определяется критич. множеством
Критерии пустых ящиков определяется критич. множеством  >С, при к-ром гипотеза H0 отвергается. Поскольку
>С, при к-ром гипотеза H0 отвергается. Поскольку  имеет при основной гипотезе H0 распределение, определяемое равномерным размещением, а при конкурирующей гипотезе Н 1- распределение, определяемое полиномиальным размещением, то можно воспользоваться предельными теоремами для
имеет при основной гипотезе H0 распределение, определяемое равномерным размещением, а при конкурирующей гипотезе Н 1- распределение, определяемое полиномиальным размещением, то можно воспользоваться предельными теоремами для  при расчете мощности
при расчете мощности  этого критерия (см. [2]).
этого критерия (см. [2]).  расположения комплектов равновероятны, а число комплектов
расположения комплектов равновероятны, а число комплектов  то при ограниченных или слабо растущих тсохраняются свойства асимптотич. нормальности и предельной пуассоновости случайных величин
то при ограниченных или слабо растущих тсохраняются свойства асимптотич. нормальности и предельной пуассоновости случайных величин 