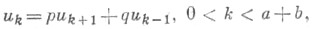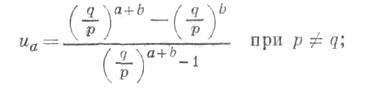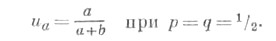|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЛУЧАЙНОЕ БЛУЖДАНИЕЗначение СЛУЧАЙНОЕ БЛУЖДАНИЕ в математической энциклопедии: - специального вида случайный процесс, к-рый можно интерпретировать как модель, описывающую перемещение частицы в нек-ром фазовом пространстве под воздействием какого-либо случайного механизма. Фазовым пространством обычно бывает d-мерное евклидово пространство или целочисленная решетка в нем. Случайные механизмы могут быть различными; чаще рассматривают С. б., порожденные суммированием независимых случайных величин или цепями Маркова. Точного общепринятого определения С. б. нет. где Xi независимы и имеют распределение Бернулли
Значение Sn можно интерпретировать как выигрыш одного из двух игроков после ппартий в игре, в к-рой этот игрок в каждой из партий выигрывает один рубль с вероятностью . и проигрывает его с вероятностью 1- р. Если игра ведется с помощью подбрасывания симметричной монеты, то следует положить р=1/2 (симметричное блуждание, см. Бернулли блуждание). При допущении, что начальный капитал 1-го игрока равен b, а начальный капитал 2-го игрока равен а, игра закончится, когда блуждающая частица (с координатами S1, S2, . . .) впервые коснется одного из уровней аили -b. В этот момент один из игроков разорится. Эта классич. задача о разорении, в к-рой барьеры в точках аи -b можно рассматривать как поглощающие.
и барьер в точке 0 можно наз. задерживающим. Существуют и другие возможности для поведения частицы вблизи барьеров.
и граничным условиям u а=0, u-b= 1. Отсюда получают
Вторая из этих формул показывает, что даже лбезобидная
|
|
|
|

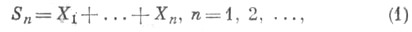
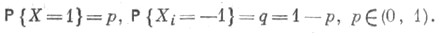
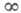 , b=0, то положение Zn+1 блуждающей частицы в момент n+1в соответствии с (1) описывается соотношением
, b=0, то положение Zn+1 блуждающей частицы в момент n+1в соответствии с (1) описывается соотношением 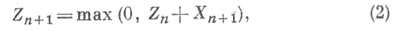
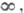 то получают задачи для С. б. с одной границей. Если а=b=
то получают задачи для С. б. с одной границей. Если а=b=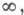 то получают неограниченное С. б. Изучение описанных С. б. происходит обычно с помощью аппарата дискретных цепей Маркова и, в частности, путем исследования соответствующих уравнений в конечных разностях. Пусть, напр., uk есть вероятность разорения 1-го игрока в задаче о разорении, если его капитал равен k,
то получают неограниченное С. б. Изучение описанных С. б. происходит обычно с помощью аппарата дискретных цепей Маркова и, в частности, путем исследования соответствующих уравнений в конечных разностях. Пусть, напр., uk есть вероятность разорения 1-го игрока в задаче о разорении, если его капитал равен k, 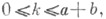 а суммарный капитал обоих игроков фиксирован и равен а+b. Тогда из формулы полной вероятности (по первому скачку) следует, что и k удовлетворяет уравнению
а суммарный капитал обоих игроков фиксирован и равен а+b. Тогда из формулы полной вероятности (по первому скачку) следует, что и k удовлетворяет уравнению