"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЛУЧАЙНАЯ ФУНКЦИЯ
Значение СЛУЧАЙНАЯ ФУНКЦИЯ в математической энциклопедии:
- функция произвольного аргумента t(заданная на множестве Тего значений и принимающая числовые значения или, более общо, значения из какого-то векторного пространства) такая, что ее значения определяются с помощью нек-ро-го испытания и в зависимости от его исхода могут быть различными, причем для них существует определенное распределение вероятностей. В теории вероятностей основное внимание обычно уделяется числовым (т. е. скалярным) С. ф. X(t);векторные же С. ф. X(t)можно рассматривать как совокупность скалярных функций 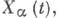 где
где  пробегает конечное или счетное множество Аномеров компонент вектора X, т. е. как числовую С. <ф.,
пробегает конечное или счетное множество Аномеров компонент вектора X, т. е. как числовую С. <ф.,  заданную на новом множестве
заданную на новом множестве 

Если множество Тконечно, то С. ф. X(t)на Тпредставляет собой конечный набор случайных величин, к-рый можно считать одной многомерной (векторной) случайной величиной, характеризуемой многомерной функцией распределения. Из числа С. ф. с бесконечным . наиболее изучен частный случай, когда tпринимает числовые (действительные) значения; в этом случае чаще всего tявляется временем, а С. ф. X(t) наз. случайным процессом (если же время . пробегает лишь целочисленные значения, то также и случайной последовательностью, или временным рядом). Если значениями аргумента tявляются точки нек-рого многомерного многообразия (напр., k-мерного евклидова пространства Rk), то С. ф. X(t)наз. случайным полем.
Распределение вероятностей значений С. ф. X(t), определенной на бесконечном множестве Т, можно охарактеризовать совокупностью конечномерных распределений вероятностей для групп случайных величин 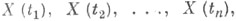 отвечающих всевозможным
отвечающих всевозможным
конечным подмножествам  элементов Т, т. е. совокупностью соответствующих конечномерных функций распределения
элементов Т, т. е. совокупностью соответствующих конечномерных функций распределения  удовлетворяющих следующим условиям согласованности:
удовлетворяющих следующим условиям согласованности:


где i1, . . ., in- произвольная перестановка индексов 1, . . ., n. Такое задание распределения вероятностей С. ф. X(t)достаточно во всех случаях, когда интересуются лишь событиями, зависящими от значений X(t)на конечных множествах значений аргумента t. Однако такое задание С. ф. не позволяет определить вероятности свойств С. ф., зависящих от ее значений на непрерывном множестве значений t, типа вероятности непрерывности или дифференцируемости С. ф. или вероятности того, что С. ф. X(t)на непрерывном множестве значений tбудет удовлетворять неравенству X(t)<a (см. Сепарабельный процесс).
Более общее задание С. ф. связано с ее описанием как совокупности случайных величин  заданных на одном и том же вероятностном пространстве
заданных на одном и том же вероятностном пространстве  (где
(где  - непустое множество точек
- непустое множество точек  - выделенная
- выделенная  алгебра подмножеств
алгебра подмножеств  а Р - заданная а
а Р - заданная а  вероятностная мера) и отвечающих всевозможным точкам tмножества Т. При таком подходе под С. ф. на множестве Тследует понимать функцию
вероятностная мера) и отвечающих всевозможным точкам tмножества Т. При таком подходе под С. ф. на множестве Тследует понимать функцию  двух переменных
двух переменных  и
и  являющуюся A-измеримой функцией
являющуюся A-измеримой функцией  при каждом фиксированном значении t(т. е. при фиксированном . обращающуюся в случайную величину, определенную на вероятностном пространстве
при каждом фиксированном значении t(т. е. при фиксированном . обращающуюся в случайную величину, определенную на вероятностном пространстве  Фиксируя значение аргумента
Фиксируя значение аргумента  функции
функции  получают числовую функцию
получают числовую функцию  на Т, называемую реализацией (или выборочной функцией, или, если t- это время, траекторией) С. ф. X(t);
на Т, называемую реализацией (или выборочной функцией, или, если t- это время, траекторией) С. ф. X(t); -алгебра
-алгебра 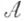 и мера Р при этом индуцируют
и мера Р при этом индуцируют  -алгебру подмножеств и определенную на ной вероятностную меру в функциональном пространстве
-алгебру подмножеств и определенную на ной вероятностную меру в функциональном пространстве  реализацией x(t), задание к-рой также можно считать эквивалентным заданию С. ф. Задание С. ф. как вероятностной меры, определенной на
реализацией x(t), задание к-рой также можно считать эквивалентным заданию С. ф. Задание С. ф. как вероятностной меры, определенной на  -алгебре подмножеств функционального пространства
-алгебре подмножеств функционального пространства  всевозможных реализаций x(t), можно рассматривать как частный случай общего задания С. ф. как функции двух переменных
всевозможных реализаций x(t), можно рассматривать как частный случай общего задания С. ф. как функции двух переменных  (где
(где  принадлежит вероятностному пространству
принадлежит вероятностному пространству  соответствующий условию, что
соответствующий условию, что  т. е. что элементарные события (точки
т. е. что элементарные события (точки  исходного вероятностного пространства) с самого начала отождествляются с реализациями х(t)С. ф. X(t);с другой стороны, можно также показать, что к такому заданию С. ф. с помощью указания вероятностной меры на
исходного вероятностного пространства) с самого начала отождествляются с реализациями х(t)С. ф. X(t);с другой стороны, можно также показать, что к такому заданию С. ф. с помощью указания вероятностной меры на  сводятся и все другие способы задания С. ф. X(t). В частности, задание совокупности всевозможных конечномерных функций распределения
сводятся и все другие способы задания С. ф. X(t). В частности, задание совокупности всевозможных конечномерных функций распределения 
 удовлетворяющих условиям согласованности (1) и (2), в силу фундаментальной теоремы Колмогорова о согласованных распределениях (см. Вероятностное пространство), определяет вероятностную меру на
удовлетворяющих условиям согласованности (1) и (2), в силу фундаментальной теоремы Колмогорова о согласованных распределениях (см. Вероятностное пространство), определяет вероятностную меру на  -алгебре подмножеств функционального пространства
-алгебре подмножеств функционального пространства  порожденной совокупностью цилиндрич. множеств вида
порожденной совокупностью цилиндрич. множеств вида  где п - произвольное целое положительное число, а В" - произвольное борелевское множество n-мерного пространства
где п - произвольное целое положительное число, а В" - произвольное борелевское множество n-мерного пространства  векторов
векторов 
Лит. см. при ст. Случайный процесс.
А. М. Яглом.

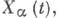 где
где  пробегает конечное или счетное множество Аномеров компонент вектора X, т. е. как числовую С. <ф.,
пробегает конечное или счетное множество Аномеров компонент вектора X, т. е. как числовую С. <ф.,  заданную на новом множестве
заданную на новом множестве 

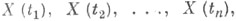 отвечающих всевозможным
отвечающих всевозможным  элементов Т, т. е. совокупностью соответствующих конечномерных функций распределения
элементов Т, т. е. совокупностью соответствующих конечномерных функций распределения  удовлетворяющих следующим условиям согласованности:
удовлетворяющих следующим условиям согласованности: 

 заданных на одном и том же вероятностном пространстве
заданных на одном и том же вероятностном пространстве  (где
(где  - непустое множество точек
- непустое множество точек  - выделенная
- выделенная  алгебра подмножеств
алгебра подмножеств  а Р - заданная а
а Р - заданная а  вероятностная мера) и отвечающих всевозможным точкам tмножества Т. При таком подходе под С. ф. на множестве Тследует понимать функцию
вероятностная мера) и отвечающих всевозможным точкам tмножества Т. При таком подходе под С. ф. на множестве Тследует понимать функцию  двух переменных
двух переменных  и
и  являющуюся A-измеримой функцией
являющуюся A-измеримой функцией  при каждом фиксированном значении t(т. е. при фиксированном . обращающуюся в случайную величину, определенную на вероятностном пространстве
при каждом фиксированном значении t(т. е. при фиксированном . обращающуюся в случайную величину, определенную на вероятностном пространстве  Фиксируя значение аргумента
Фиксируя значение аргумента  функции
функции  получают числовую функцию
получают числовую функцию  на Т, называемую реализацией (или выборочной функцией, или, если t- это время, траекторией) С. ф. X(t);
на Т, называемую реализацией (или выборочной функцией, или, если t- это время, траекторией) С. ф. X(t); -алгебра
-алгебра 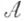 и мера Р при этом индуцируют
и мера Р при этом индуцируют  -алгебру подмножеств и определенную на ной вероятностную меру в функциональном пространстве
-алгебру подмножеств и определенную на ной вероятностную меру в функциональном пространстве  реализацией x(t), задание к-рой также можно считать эквивалентным заданию С. ф. Задание С. ф. как вероятностной меры, определенной на
реализацией x(t), задание к-рой также можно считать эквивалентным заданию С. ф. Задание С. ф. как вероятностной меры, определенной на  -алгебре подмножеств функционального пространства
-алгебре подмножеств функционального пространства  всевозможных реализаций x(t), можно рассматривать как частный случай общего задания С. ф. как функции двух переменных
всевозможных реализаций x(t), можно рассматривать как частный случай общего задания С. ф. как функции двух переменных  (где
(где  принадлежит вероятностному пространству
принадлежит вероятностному пространству  соответствующий условию, что
соответствующий условию, что  т. е. что элементарные события (точки
т. е. что элементарные события (точки  исходного вероятностного пространства) с самого начала отождествляются с реализациями х(t)С. ф. X(t);с другой стороны, можно также показать, что к такому заданию С. ф. с помощью указания вероятностной меры на
исходного вероятностного пространства) с самого начала отождествляются с реализациями х(t)С. ф. X(t);с другой стороны, можно также показать, что к такому заданию С. ф. с помощью указания вероятностной меры на  сводятся и все другие способы задания С. ф. X(t). В частности, задание совокупности всевозможных конечномерных функций распределения
сводятся и все другие способы задания С. ф. X(t). В частности, задание совокупности всевозможных конечномерных функций распределения 
 удовлетворяющих условиям согласованности (1) и (2), в силу фундаментальной теоремы Колмогорова о согласованных распределениях (см. Вероятностное пространство), определяет вероятностную меру на
удовлетворяющих условиям согласованности (1) и (2), в силу фундаментальной теоремы Колмогорова о согласованных распределениях (см. Вероятностное пространство), определяет вероятностную меру на  -алгебре подмножеств функционального пространства
-алгебре подмножеств функционального пространства  порожденной совокупностью цилиндрич. множеств вида
порожденной совокупностью цилиндрич. множеств вида  где п - произвольное целое положительное число, а В" - произвольное борелевское множество n-мерного пространства
где п - произвольное целое положительное число, а В" - произвольное борелевское множество n-мерного пространства  векторов
векторов 