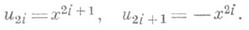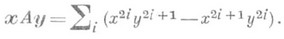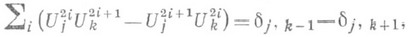" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

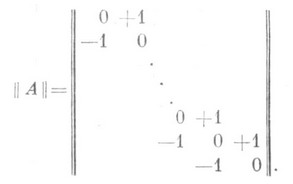
СИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО

Значение СИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии:

нечетномерное проективное пространство P_2n+1 над полем kс заданной в нем инволюционной корреляцией - нульсистемой; обозначается Sp_2n+1.

Пусть характеристика поля kни равна 2. Абсолютная нульгсистема в Sp_2n+1 всегда может быть записана в виде u_i=a_ijx^j, где ||a_ij|| - кососимметрич. матрица (a_ij=-a_ji). В векторной форме абсолютная нуль-система может быть записана в виде и=А x, где А - ко-сосимметрич. оператор, матрица к-рого надлежащим выбором базиса приводится к виду

В этом случае абсолютная нуль-система принимает канонич. вид:

Абсолютная нуль-система порождает билинейную форму, к-рая записывается в канонич. виде:

Коллинеации пространства Sp_2n+1, перестановочные с его нуль-системой, наз. симплектическими преобразованиями; операторы, определяющие эти коллинеации,- симплектическими. Для указанной выше канонич. формы матрицы ||A|| определяется (2n+2)-матрица симплектич. оператора U, элементы к-рой удовлетворяют условиям

где d_a,b - символ Кронекера, а матрица такого оператора Uназ. симплектической; ее определитель равен единице. Симплектич. преобразования образуют группу, являющуюся группой Ли.

Всякая точка пространства Sp_2n+1 лежит в (2п-1) плоскости, соответствующей ей в абсолютной нуль-системе. Можно определить также и нулевые m-плоскости в Sp_2n+1. Многообразие нулевых прямых пространства Sp_2n+1 наз. его абсолютным линейным комплексом. В связи с этим симплектич. группа наз. также группой линейного комплекса, или комплекс-группой.

Всякая пара прямых и соответствующих в нуль-системе двух (2n-1)-плоскостей определяют единственный в пространстве Sp_2n+1 симплектич. инвариант относительно группы симплектич. преобразований этого пространства. Через каждую точку обеих прямых проходит трансверсаль этих прямых и (2n-1)-плоскостей так, что определяет проективные четверки точек. Это составляет геометрический смысл симплектического инварианта, который утверждает равенство двойных отношений получаемых четверок точек.

Симплектич. 3-пространство допускает интерпретацию в гиперболич. пространстве, что указывает, в частности, на связь симплектич. пространств с гиперболическими. Так, группа симплектич. преобразований пространства Sp₃ изоморфна группе движений гиперболич. пространства ²S₄. В этой интерпретации симплектич. инвариант связан с расстоянием между точками гиперболич. пространства.

Лит.; [1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Л. А. Сидоров.