|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СИМПЛЕКСНЫЙ МЕТОДЗначение СИМПЛЕКСНЫЙ МЕТОД в математической энциклопедии: симплекс - метод, метод последовательного улучшения плана,- метод решения общей задачи линейного программирования: где С. м.- наиболее распространенный метод линейного программирования (л. п.). Он состоит в движении по соседним вершинам многогранного множества задачи л. п., определяемого ее ограничениями, и реализуется в виде конечной последовательности итераций. Базисом вершины х=( х 1, . . ., х п).многогранного множества задачи наз. такая система тлинейно независимых векторов (в частности, г,-0=ж 5;- базисные компоненты вершины х), и параметров Если остальные компоненты xk - нули, Вершина х' имеет базис А x', отличающийся от А х тем, что Случай (1) означает, что вдоль каждого ребра многогранного множества задачи, выходящего из вершины х, целевая функция задачи не возрастает. Случаи (2) и (3) соответствуют наличию ребра, вдоль к-рого целевая функция возрастает, причем в случае (2) это ребро - луч, а в случае (3) - отрезок, другой конец к-рого - вершина х'. Итерации проводятся до получения оптимальной вершины либо до выяснения неразрешимости задачи л. п. Программная реализация С. <м., рассчитанная на задачи достаточно большого размера, обычно основывается на иной его алгоритмич. реализации, в к-рой основой исходной информации для каждой итерации служит обратная матрица Важная часть алгоритма С. м. - стратегия выбора вектора А k для включения в базис. С одной стороны, она должна способствовать сокращению информации, необходимой для хранения Существуют программные реализации С. м., позволяющие решать на ЭВМ задачи л. п. с мало заполненной матрицей условий при тпорядка тысяч и ппорядка десятков тысяч. Разработаны многочисленные варианты С. м., учитывающие особенности различных специальных классов задач л. п. (блочные задачи, задачи транспортного типа и др.). Несмотря на то, что С. м. теоретически не достаточно эффективен (он имеет экспоненциальную оценку трудоемкости на всем классе задач л. п., хотя алгоритмич. сложность этого класса всего лишь полиномиальна), опыт его применения и сравнения с другими методами позволяет сделать вывод, что для него пока (1983) нет серьезного конкурента. Лит.:[1] Юдин Д. В., Гольштейн К. Г., Линейное программирование, М., 1963; [2] Данциг Дж., Линейное программирование, его применения и обобщения, пер. с англ., М., 1966; [3] Ашманов С. А., Линейное программирование, М., 1981. Е. Г. Голъштейн. |
|
|
|




 , что xj=0, если
, что xj=0, если  . Исходная информация для каждой итерации С. м. складывается из базиса
. Исходная информация для каждой итерации С. м. складывается из базиса  вершины х, параметров xij, определяемых из соотношений
вершины х, параметров xij, определяемых из соотношений 

 (1), то х- искомое решение задачи л. п. В противном случае выбирается отрицательный параметр Dk. Отсутствие среди х ik, i=1, . . ., m, положительных величин (2) указывает на неразрешимость задачи л. п., обусловленную неограниченностью целевой функции задачи на ее многогранном множестве. В случае положительности нек-рых х ik(3) вершина хзаменяется вершиной x'=x+qxk, где
(1), то х- искомое решение задачи л. п. В противном случае выбирается отрицательный параметр Dk. Отсутствие среди х ik, i=1, . . ., m, положительных величин (2) указывает на неразрешимость задачи л. п., обусловленную неограниченностью целевой функции задачи на ее многогранном множестве. В случае положительности нек-рых х ik(3) вершина хзаменяется вершиной x'=x+qxk, где 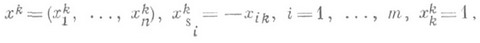

 заменен на А k. Параметры
заменен на А k. Параметры  и
и  , связанные с А x', определяются по простым рекуррентным формулам, исходя из х ij и Dj.
, связанные с А x', определяются по простым рекуррентным формулам, исходя из х ij и Dj. базиса А х (метод обратной матрицы). Она предназначена для задач л. п., матрица условий А=( А 1 А 2. . .А п).к-рых обладает свойством слабой заполненности (число ненулевых а ij мало по сравнению с тп). Слабо заполненные матрицы хранятся в запоминающих устройствах ЭВМ в компактном виде, когда фиксированы лишь ненулевые элементы и их позиции. Разработаны специальные приемы хранения обратного базиса, направленные на сокращение информации, необходимой для восстановления
базиса А х (метод обратной матрицы). Она предназначена для задач л. п., матрица условий А=( А 1 А 2. . .А п).к-рых обладает свойством слабой заполненности (число ненулевых а ij мало по сравнению с тп). Слабо заполненные матрицы хранятся в запоминающих устройствах ЭВМ в компактном виде, когда фиксированы лишь ненулевые элементы и их позиции. Разработаны специальные приемы хранения обратного базиса, направленные на сокращение информации, необходимой для восстановления  . Они основаны на представлении
. Они основаны на представлении  в виде произведения матричных множителей (мультипликаторов), отличающихся от единичной матрицы лишь одним столбцом. Заполненность нетривиальных столбцов мультипликаторов зависит от порядка введения векторов в базис. Поэтому после накопления нек-рого числа мультипликаторов организуется т. н. повторение, в результате к-рого образуется более экономное мультипликативное представление
в виде произведения матричных множителей (мультипликаторов), отличающихся от единичной матрицы лишь одним столбцом. Заполненность нетривиальных столбцов мультипликаторов зависит от порядка введения векторов в базис. Поэтому после накопления нек-рого числа мультипликаторов организуется т. н. повторение, в результате к-рого образуется более экономное мультипликативное представление  .
. ; с другой стороны - препятствовать попаданию в плохо обусловленный базис.
; с другой стороны - препятствовать попаданию в плохо обусловленный базис.