|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЖИМАЮЩИХ ОТОБРАЖЕНИИ ПРИНЦИПЗначение СЖИМАЮЩИХ ОТОБРАЖЕНИИ ПРИНЦИП в математической энциклопедии: сжатых отображении принцип,- теорема, утверждающая существование и единственность неподвижной точки у отображения f полного метрич. пространства (X,r) (или замкнутого подмножества такого пространства) в себя, если для любых х', х" выполняется неравенство где 0<q<1. Этот принцип широко используется для доказательства существования и единственности решения не только уравнения вида f(x)=x, но и уравнений f(x)=y путем замены такого уравнения на эквивалентное: Схема применения С. о. п. обычно такова: исходя из свойств отображением f находят сначала замкнутое множество В общем случае условие (1) нельзя заменить условием однако если это условие выполняется на компактном множестве K, к-рое f отображает в себя, то условие (2) обеспечивает у f существование единственной неподвижной точки Имеет место следующее обобщение С. о. п. Пусть снова f отображает полное метрич. пространство Xв себя и при Лит.:[1] К о л м о г о р о в А. Н., Ф о м и н С. В., Элементы теории фуннций и функционального анализа, 5 изд., М., 1981; [2] К р а с н о с е л ь с к и й М. А. [и др.], Приближенное решение операторных уравнений, М., 1969; [3] Л ю с т е р н и к Л. А., С о б о л е в В. И., Элементы функционального анализа, 2 изд., М., 1965; [4] Т р е н о г и н В. А., Функциональный анализ, М., 1980. В. И. Соболев. |
|
|
|

 (1)
(1) , где
, где  .
. , обычно замкнутый шар, такое, что
, обычно замкнутый шар, такое, что  , а затем доказывают, что на этом множестве f является отображением сжатия. После этого, отправляясь от произвольного элемента
, а затем доказывают, что на этом множестве f является отображением сжатия. После этого, отправляясь от произвольного элемента 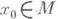 , строят последовательность {sn}, xn=f(xn-1), n=1, 2, . . ., принадлежащую М, к-рая сходится к нек-рому элементу
, строят последовательность {sn}, xn=f(xn-1), n=1, 2, . . ., принадлежащую М, к-рая сходится к нек-рому элементу  . Это и будет единственное решение уравнения f(x)=x, а х п будут последовательными приближениями решения.
. Это и будет единственное решение уравнения f(x)=x, а х п будут последовательными приближениями решения. (2)
(2) .
.
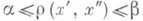 , где
, где  для
для  . Тогда отображение f имеет на Xединственную неподвижную точку.
. Тогда отображение f имеет на Xединственную неподвижную точку.