"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СЖАТИЕ
Значение СЖАТИЕ в математической энциклопедии:
алгебры Ли, стягивание алгебры Ли,- операция, противоположная деформации алгебры Ли. Пусть  - конечномерная вещественная алгебра Ли,
- конечномерная вещественная алгебра Ли,  - набор ее структурных констант в фиксированном базисе е 1, . . ., е n и А (t),
- набор ее структурных констант в фиксированном базисе е 1, . . ., е n и А (t), ,- кривая в группе невырожденных линейных преобразований пространства
,- кривая в группе невырожденных линейных преобразований пространства  такая, что А(1)=Е. Пусть
такая, что А(1)=Е. Пусть  и
и  - структурные константы алгебры
- структурные константы алгебры  в базисе
в базисе  . Если
. Если  при
при  стремятся к нек-рому пределу
стремятся к нек-рому пределу  , то алгебра
, то алгебра  , определяемая этими константами в исходном базисе, наз. сжатием исходной алгебры
, определяемая этими константами в исходном базисе, наз. сжатием исходной алгебры  . Сжатие
. Сжатие  также является алгеброй Ли, причем
также является алгеброй Ли, причем  можно получить путем деформации алгебры
можно получить путем деформации алгебры  . Если
. Если  - алгебра Ли группы Ли G, то группу Ли
- алгебра Ли группы Ли G, то группу Ли  , соответствующую
, соответствующую  также наз. сжатием группы G.
также наз. сжатием группы G.
Хотя  эти алгебры, вообще говоря, не изоморфны: напр., если A(t)=tE, то
эти алгебры, вообще говоря, не изоморфны: напр., если A(t)=tE, то  , так что при таком С. предельная алгебра всегда коммутативна. Естественное обобщение этого примера состоит в следующем: пусть
, так что при таком С. предельная алгебра всегда коммутативна. Естественное обобщение этого примера состоит в следующем: пусть  - подалгебра в
- подалгебра в  - дополнительное к
- дополнительное к 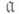 подпространство, причем
подпространство, причем 
 , и A(t)v=v для
, и A(t)v=v для  для
для  . Тогда в пределе
. Тогда в пределе  становился коммутативным идеалом алгебры
становился коммутативным идеалом алгебры  , в то время как умножение в
, в то время как умножение в  и присоединенное действие алгебры
и присоединенное действие алгебры  на
на  остаются неизменными.
остаются неизменными.
В частности, пусть G - группа Лоренца,  - ее алгебра Ли,
- ее алгебра Ли,  - подалгебра, соответствующая подгруппе вращений 3-мерного пространства. Тогда описанное С. алгебры
- подалгебра, соответствующая подгруппе вращений 3-мерного пространства. Тогда описанное С. алгебры  дает алгебру Ли группы Галилея
дает алгебру Ли группы Галилея  (см. Галилея преобразование, Лоренца преобразование). Соответственно алгебра Лоренца является деформацией алгебры Галилея и можно показать, что комплексификация алгебры Галилея других деформаций не имеет; в вещественном случае алгебру Галилея можно получить также С. ортогональной алгебры Ли so(4). Эквивалентный способ получения алгебры Галилея из алгебры Лоренца состоит в том, чтобы определить алгебру Лоренца как алгебру, сохраняющую форму Минковского x2+y2+z2 -с 2t2, и затем устремить скорость света ск
(см. Галилея преобразование, Лоренца преобразование). Соответственно алгебра Лоренца является деформацией алгебры Галилея и можно показать, что комплексификация алгебры Галилея других деформаций не имеет; в вещественном случае алгебру Галилея можно получить также С. ортогональной алгебры Ли so(4). Эквивалентный способ получения алгебры Галилея из алгебры Лоренца состоит в том, чтобы определить алгебру Лоренца как алгебру, сохраняющую форму Минковского x2+y2+z2 -с 2t2, и затем устремить скорость света ск  . Пока
. Пока  , возникающие алгебры изоморфны
, возникающие алгебры изоморфны  . Аналогично, деформируя алгебру Пуанкаре (неоднородную алгебру Лоренца), можно получить алгебры де Ситтера so (4,1) и so (3,2) движений пространства постоянной кривизны. Соответственно, устремляя кривизну к 0, получают группу Пуанкаре как С. групп де Ситтера.
. Аналогично, деформируя алгебру Пуанкаре (неоднородную алгебру Лоренца), можно получить алгебры де Ситтера so (4,1) и so (3,2) движений пространства постоянной кривизны. Соответственно, устремляя кривизну к 0, получают группу Пуанкаре как С. групп де Ситтера.
Связь между этими алгебрами продолжается на представления. Если, как в описанных примерах, существует матрица  , то каждое представление Sалгебры
, то каждое представление Sалгебры  порождает представление
порождает представление  сжатой алгебры по формуле
сжатой алгебры по формуле

для любого  Обратная операция (деформация представлений), вообще говоря, невозможна.
Обратная операция (деформация представлений), вообще говоря, невозможна.
Лит.:[1] Б а р у т А., Р о н ч к а Р., Теория представлений групп и ее приложения, пер. с англ., т. 1, М., 1980; [2] I n о n u Е., W i g n е r Е. P., "Proc. Nat. Acad. Sci. USA", 1953, v. 39, p. 510-24; [3] S a 1 e t a n E. J., "J. Math. Phys.", 1961, v. 2, p. 1-22. А. К. Толпыго.

 - конечномерная вещественная алгебра Ли,
- конечномерная вещественная алгебра Ли,  - набор ее структурных констант в фиксированном базисе е 1, . . ., е n и А (t),
- набор ее структурных констант в фиксированном базисе е 1, . . ., е n и А (t), ,- кривая в группе невырожденных линейных преобразований пространства
,- кривая в группе невырожденных линейных преобразований пространства  такая, что А(1)=Е. Пусть
такая, что А(1)=Е. Пусть  и
и  - структурные константы алгебры
- структурные константы алгебры  в базисе
в базисе  . Если
. Если  при
при  стремятся к нек-рому пределу
стремятся к нек-рому пределу  , то алгебра
, то алгебра  , определяемая этими константами в исходном базисе, наз. сжатием исходной алгебры
, определяемая этими константами в исходном базисе, наз. сжатием исходной алгебры  . Сжатие
. Сжатие  также является алгеброй Ли, причем
также является алгеброй Ли, причем  можно получить путем деформации алгебры
можно получить путем деформации алгебры  . Если
. Если  - алгебра Ли группы Ли G, то группу Ли
- алгебра Ли группы Ли G, то группу Ли  , соответствующую
, соответствующую  также наз. сжатием группы G.
также наз. сжатием группы G. эти алгебры, вообще говоря, не изоморфны: напр., если A(t)=tE, то
эти алгебры, вообще говоря, не изоморфны: напр., если A(t)=tE, то  , так что при таком С. предельная алгебра всегда коммутативна. Естественное обобщение этого примера состоит в следующем: пусть
, так что при таком С. предельная алгебра всегда коммутативна. Естественное обобщение этого примера состоит в следующем: пусть  - подалгебра в
- подалгебра в  - дополнительное к
- дополнительное к 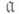 подпространство, причем
подпространство, причем 
 , и A(t)v=v для
, и A(t)v=v для  для
для  . Тогда в пределе
. Тогда в пределе  становился коммутативным идеалом алгебры
становился коммутативным идеалом алгебры  , в то время как умножение в
, в то время как умножение в  и присоединенное действие алгебры
и присоединенное действие алгебры  на
на  остаются неизменными.
остаются неизменными. - ее алгебра Ли,
- ее алгебра Ли,  - подалгебра, соответствующая подгруппе вращений 3-мерного пространства. Тогда описанное С. алгебры
- подалгебра, соответствующая подгруппе вращений 3-мерного пространства. Тогда описанное С. алгебры  дает алгебру Ли группы Галилея
дает алгебру Ли группы Галилея  (см. Галилея преобразование, Лоренца преобразование). Соответственно алгебра Лоренца является деформацией алгебры Галилея и можно показать, что комплексификация алгебры Галилея других деформаций не имеет; в вещественном случае алгебру Галилея можно получить также С. ортогональной алгебры Ли so(4). Эквивалентный способ получения алгебры Галилея из алгебры Лоренца состоит в том, чтобы определить алгебру Лоренца как алгебру, сохраняющую форму Минковского x2+y2+z2 -с 2t2, и затем устремить скорость света ск
(см. Галилея преобразование, Лоренца преобразование). Соответственно алгебра Лоренца является деформацией алгебры Галилея и можно показать, что комплексификация алгебры Галилея других деформаций не имеет; в вещественном случае алгебру Галилея можно получить также С. ортогональной алгебры Ли so(4). Эквивалентный способ получения алгебры Галилея из алгебры Лоренца состоит в том, чтобы определить алгебру Лоренца как алгебру, сохраняющую форму Минковского x2+y2+z2 -с 2t2, и затем устремить скорость света ск  . Пока
. Пока  , возникающие алгебры изоморфны
, возникающие алгебры изоморфны  . Аналогично, деформируя алгебру Пуанкаре (неоднородную алгебру Лоренца), можно получить алгебры де Ситтера so (4,1) и so (3,2) движений пространства постоянной кривизны. Соответственно, устремляя кривизну к 0, получают группу Пуанкаре как С. групп де Ситтера.
. Аналогично, деформируя алгебру Пуанкаре (неоднородную алгебру Лоренца), можно получить алгебры де Ситтера so (4,1) и so (3,2) движений пространства постоянной кривизны. Соответственно, устремляя кривизну к 0, получают группу Пуанкаре как С. групп де Ситтера. , то каждое представление Sалгебры
, то каждое представление Sалгебры  порождает представление
порождает представление  сжатой алгебры по формуле
сжатой алгебры по формуле 
 Обратная операция (деформация представлений), вообще говоря, невозможна.
Обратная операция (деформация представлений), вообще говоря, невозможна.