"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕЗначение БИРАЦИОНАЛЬНОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
бирациональный изоморфизм,- рациональное отображение алгебраич. многообразий, индуцирующее изоморфизм их полей рациональных функций. В более общем смысле, рациональное отображение схем  наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества  , что , что 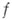 определено на определено на  и осуществляет изоморфизм подсхем и осуществляет изоморфизм подсхем  б) если б) если  - множества общих точек неприводимых компонент соответственно схем - множества общих точек неприводимых компонент соответственно схем 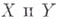 , то f индуцирует биективное соответствие множеств , то f индуцирует биективное соответствие множеств  и изоморфизм .локальных колец и изоморфизм .локальных колец  для каждого для каждого  . .
Если схемы 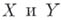 неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на 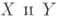 В этом случае Б. о. f: В этом случае Б. о. f:  индуцирует, согласно условию б), изоморфизм полей рациональных функций: индуцирует, согласно условию б), изоморфизм полей рациональных функций:
Схемы 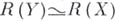 Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о. Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.  . Частный случай Б. о.- бирационалъный морфизм. . Частный случай Б. о.- бирационалъный морфизм.
Простейшим Б. о. является моноидалъное преобразование с неособым центром. Для гладких полных многообразий размерности 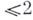 всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым. всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.
Лит.:[1] Шафаревич II. Р., Основы алгебраической геометрии, М., 1972. И. В. Долгачее, В. А. Исковских.
|

 наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества
наз. бирациональным отображение м, если оно удовлетворяет одному из. следующих эквивалентных условий: а) существуют такие плотные открытые множества  , что
, что 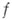 определено на
определено на  и осуществляет изоморфизм подсхем
и осуществляет изоморфизм подсхем  б) если
б) если  - множества общих точек неприводимых компонент соответственно схем
- множества общих точек неприводимых компонент соответственно схем 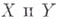 , то f индуцирует биективное соответствие множеств
, то f индуцирует биективное соответствие множеств  и изоморфизм .локальных колец
и изоморфизм .локальных колец  для каждого
для каждого  .
.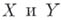 неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на
неприводимы и приведены, то локальные кольца их общих точек отождествляются с полями рациональных функций соответственно на 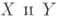 В этом случае Б. о. f:
В этом случае Б. о. f:  индуцирует, согласно условию б), изоморфизм полей рациональных функций:
индуцирует, согласно условию б), изоморфизм полей рациональных функций: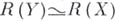 Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.
Xи Yназ. бирационально эквивалентными, или бирационально изоморфными, если существует Б. о.  . Частный случай Б. о.- бирационалъный морфизм.
. Частный случай Б. о.- бирационалъный морфизм.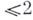 всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.
всякое Б. о. может быть представлено в виде композиции таких преобразований и обратных к ним. В общем случае вопрос остается (к 1977) открытым.