|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СВЯЗНОСТИ ОБЪЕКТЗначение СВЯЗНОСТИ ОБЪЕКТ в математической энциклопедии: - дифференциально-геометрический объект на гладком главном расслоенном пространстве Р, спомощью к-рого задается горизонтальное распределение Они выражены с помощью 1-форм на R0 (Р), входящие в структурные уравнения для форм wi, wr, составляющих дуальный кобазис к { е i еr}: С. о. определяет также связности формуq согласно формуле Напр., пусть Рявляется пространством аффинных реперов в касательных пространствах n-мерного гладкого многообразия М. Тогда вторые из уравнений (2) имеют вид и (1) сводятся к При параллельном перенесении должно быть следует из условия инвариантности перенесения. Ю. Г. Лумисте. |
|
|
|

 связности в Р. Пусть R0 (Р)является расслоением всех таких реперов в касательных к Рпространствах, что первые r векторов е 1, . . ., е r касательны к слою и порождаются определенными r базисными элементами в алгебре Ли структурной группы G пространства Р, r=dimG. С. о. составляют тогда функции
связности в Р. Пусть R0 (Р)является расслоением всех таких реперов в касательных к Рпространствах, что первые r векторов е 1, . . ., е r касательны к слою и порождаются определенными r базисными элементами в алгебре Ли структурной группы G пространства Р, r=dimG. С. о. составляют тогда функции  на R0 (Р)такие, что подпространство распределения
на R0 (Р)такие, что подпространство распределения  натянуто на векторы
натянуто на векторы  (r, s=1,. . ., r; i, j,. . . = r+1,. . ., r+n). Условия, к-рым должны удовлетворить функции
(r, s=1,. . ., r; i, j,. . . = r+1,. . ., r+n). Условия, к-рым должны удовлетворить функции 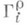 на R0 (Р), чтобы они составили С. о., следующие:
на R0 (Р), чтобы они составили С. о., следующие: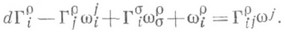 (1)
(1) (2)
(2)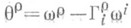 и кривизны форму
и кривизны форму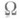 согласно формулам
согласно формулам 



 . Если на Мвыбрана локальная карта и в ее области сделан переход к натуральному реперу карты, то
. Если на Мвыбрана локальная карта и в ее области сделан переход к натуральному реперу карты, то  и параллельное перенесение определяется с помощью
и параллельное перенесение определяется с помощью  . Классич. определение С. о. аффинной связности на Мкак совокупности функций
. Классич. определение С. о. аффинной связности на Мкак совокупности функций 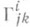 , заданных на области каждой карты и преобразующихся при переходе к координатам другой карты по формулам
, заданных на области каждой карты и преобразующихся при переходе к координатам другой карты по формулам 