"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
СВОБОДНОЕ МНОЖЕСТВОЗначение СВОБОДНОЕ МНОЖЕСТВО в математической энциклопедии:
в векторном пространстве Х над полем K - то же, что линейно независимая система векторов из X, т. е. множество элементов  , такое, что соотношение , такое, что соотношение 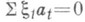 , где , где 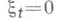 для всех кроме конечного числа индексов t,влечет для всех кроме конечного числа индексов t,влечет 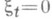 для всех t. Несвободное множество наз. также з а в и с и м ы м. для всех t. Несвободное множество наз. также з а в и с и м ы м.
С в о б о д н о е м н о ж е с т в о в топологическом векторном пространстве X над полем К(топологически свободное множество) - множество 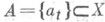 такое, что для любого такое, что для любого 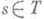 замкнутое подпространство, порожденное точками замкнутое подпространство, порожденное точками 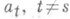 , не содержит а s. Топологически С. м. является С. м. векторного пространства; обратное неверно. Напр., в нормированном пространстве Снепрерывных функций на [0, 1] функции , не содержит а s. Топологически С. м. является С. м. векторного пространства; обратное неверно. Напр., в нормированном пространстве Снепрерывных функций на [0, 1] функции 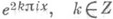 , образуют топологически С. м. в отличие от функций , образуют топологически С. м. в отличие от функций 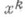 (поскольку хсодержится в замкнутом подпространстве, порожденном (поскольку хсодержится в замкнутом подпространстве, порожденном 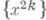 ). ).
Совокупность всех (топологически) С. м. в X, вообще говоря, не индуктивна относительно включения; кроме того, она не обязательно содержит максимальное топологически С. м. Напр., пусть X - пространство над 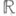 , образованное непрерывными функциями и наделенное отделимой топологией: соответствующая фундаментальная система окрестностей нуля в Xсостоит из уравновешенных поглощающих множеств , образованное непрерывными функциями и наделенное отделимой топологией: соответствующая фундаментальная система окрестностей нуля в Xсостоит из уравновешенных поглощающих множеств 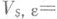 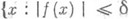 всюду вне (зависящего от f) открытого множества меры всюду вне (зависящего от f) открытого множества меры 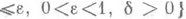 . Тогда каждый непрерывный линейный функционал равен нулю и в Xне существует максимального С. м. . Тогда каждый непрерывный линейный функционал равен нулю и в Xне существует максимального С. м.
Для того чтобы Абыло (топологически) С. м. в ослабленной топологии s( Х, X* )в X, необходимо и достаточно, чтобы для каждого t существовал элемент 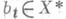 такой, что такой, что 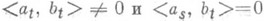 для всех для всех 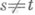 Для локально выпуклого пространства С. м. в ослабленной топологии является С. м. и в исходной топологии. Для локально выпуклого пространства С. м. в ослабленной топологии является С. м. и в исходной топологии.
М. И. Войцеховский.
|

 , такое, что соотношение
, такое, что соотношение 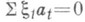 , где
, где 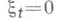 для всех кроме конечного числа индексов t,влечет
для всех кроме конечного числа индексов t,влечет 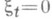 для всех t. Несвободное множество наз. также з а в и с и м ы м.
для всех t. Несвободное множество наз. также з а в и с и м ы м.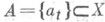 такое, что для любого
такое, что для любого 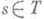 замкнутое подпространство, порожденное точками
замкнутое подпространство, порожденное точками 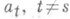 , не содержит а s. Топологически С. м. является С. м. векторного пространства; обратное неверно. Напр., в нормированном пространстве Снепрерывных функций на [0, 1] функции
, не содержит а s. Топологически С. м. является С. м. векторного пространства; обратное неверно. Напр., в нормированном пространстве Снепрерывных функций на [0, 1] функции 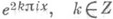 , образуют топологически С. м. в отличие от функций
, образуют топологически С. м. в отличие от функций 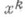 (поскольку хсодержится в замкнутом подпространстве, порожденном
(поскольку хсодержится в замкнутом подпространстве, порожденном 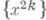 ).
).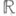 , образованное непрерывными функциями и наделенное отделимой топологией: соответствующая фундаментальная система окрестностей нуля в Xсостоит из уравновешенных поглощающих множеств
, образованное непрерывными функциями и наделенное отделимой топологией: соответствующая фундаментальная система окрестностей нуля в Xсостоит из уравновешенных поглощающих множеств 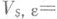
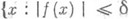 всюду вне (зависящего от f) открытого множества меры
всюду вне (зависящего от f) открытого множества меры 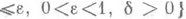 . Тогда каждый непрерывный линейный функционал равен нулю и в Xне существует максимального С. м.
. Тогда каждый непрерывный линейный функционал равен нулю и в Xне существует максимального С. м.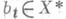 такой, что
такой, что 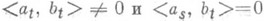 для всех
для всех 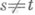 Для локально выпуклого пространства С. м. в ослабленной топологии является С. м. и в исходной топологии.
Для локально выпуклого пространства С. м. в ослабленной топологии является С. м. и в исходной топологии.