"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БИНАРНОЕ ОТНОШЕНИЕ
Значение БИНАРНОЕ ОТНОШЕНИЕ в математической энциклопедии:
двуместный предикат на заданном множестве. Под Б. о. иногда понимают подмножество множества  упорядоченных пар (а, 6) элементов заданного множества А. Б. о.- частный случай отношения. Пусть
упорядоченных пар (а, 6) элементов заданного множества А. Б. о.- частный случай отношения. Пусть  . Если
. Если 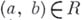 , то говорят, что элемент "находится в бинарном отношении R к элементу b. Вместо
, то говорят, что элемент "находится в бинарном отношении R к элементу b. Вместо  пишут также
пишут также  .
.
Пустое подмножество  в
в  и само множество
и само множество  наз., соответственно, нуль-отношением и универсальным отношением в множестве А. Диагональ множества
наз., соответственно, нуль-отношением и универсальным отношением в множестве А. Диагональ множества  , т. е. множество
, т. е. множество  есть отношение равенст-в а, или единичное бинарное отношение в А.
есть отношение равенст-в а, или единичное бинарное отношение в А.
Пусть  - Б. о. в множестве А. Наряду с теоретико-множественными операциями объединения
- Б. о. в множестве А. Наряду с теоретико-множественными операциями объединения 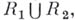 пересечения
пересечения  и дополнения
и дополнения 
 для Б. о. рассматривают также операцию обращения:
для Б. о. рассматривают также операцию обращения:

и операцию умножения:

Б. о.  наз. обратным для R. Умножение Б. о. ассоциативно, но, вообще говоря, не коммутативно.
наз. обратным для R. Умножение Б. о. ассоциативно, но, вообще говоря, не коммутативно.
Б. о. R в A называется: а) рефлексивным, если  ; б) транзитивным, если
; б) транзитивным, если  ; в) симметричным, если
; в) симметричным, если  ; г) антисимметричным, если
; г) антисимметричным, если  . Если Б. о. R обладает нек-рым из свойств а), б), в), г), то обратное отношение
. Если Б. о. R обладает нек-рым из свойств а), б), в), г), то обратное отношение  обладает этим же свойством. Б. р.
обладает этим же свойством. Б. р. 
 наз. функциональным, если
наз. функциональным, если 

Наиболее важными типами Б. о. являются эквивалентности, порядки (линейные и частичные) и функциональные отношения. д. м. Смирнов.

 упорядоченных пар (а, 6) элементов заданного множества А. Б. о.- частный случай отношения. Пусть
упорядоченных пар (а, 6) элементов заданного множества А. Б. о.- частный случай отношения. Пусть  . Если
. Если 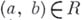 , то говорят, что элемент "находится в бинарном отношении R к элементу b. Вместо
, то говорят, что элемент "находится в бинарном отношении R к элементу b. Вместо  пишут также
пишут также  .
. в
в  и само множество
и само множество  наз., соответственно, нуль-отношением и универсальным отношением в множестве А. Диагональ множества
наз., соответственно, нуль-отношением и универсальным отношением в множестве А. Диагональ множества  , т. е. множество
, т. е. множество  есть отношение равенст-в а, или единичное бинарное отношение в А.
есть отношение равенст-в а, или единичное бинарное отношение в А. - Б. о. в множестве А. Наряду с теоретико-множественными операциями объединения
- Б. о. в множестве А. Наряду с теоретико-множественными операциями объединения 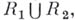 пересечения
пересечения  и дополнения
и дополнения 
 для Б. о. рассматривают также операцию обращения:
для Б. о. рассматривают также операцию обращения: 

 наз. обратным для R. Умножение Б. о. ассоциативно, но, вообще говоря, не коммутативно.
наз. обратным для R. Умножение Б. о. ассоциативно, но, вообще говоря, не коммутативно. ; б) транзитивным, если
; б) транзитивным, если  ; в) симметричным, если
; в) симметричным, если  ; г) антисимметричным, если
; г) антисимметричным, если  . Если Б. о. R обладает нек-рым из свойств а), б), в), г), то обратное отношение
. Если Б. о. R обладает нек-рым из свойств а), б), в), г), то обратное отношение  обладает этим же свойством. Б. р.
обладает этим же свойством. Б. р. 
 наз. функциональным, если
наз. функциональным, если 
