САМОСОПРЯЖЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ

Значение САМОСОПРЯЖЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ в математической энциклопедии:

- линейное преобразование евклидова или унитарного пространства, совпадающее со своим сопряженным линейным преобразованием. В евклидовом пространстве С. л. п. наз. также симметрическим, а в унитарном пространстве - эрмитовым. Необходимое и достаточное условие самосопряженности линейного преобразования конечномерного пространства состоит в том, что его матрица Ав произвольном ортонормированном базисе совпадает с сопряженной матрицей А*, т. е. является симметрич. матрицей (в евклидовом случае) или эрмитовой матрицей (в унитарном случае). Собственные значения С. л. п. действительны (даже в унитарном случае), а собственные векторы, отвечающие различным собственным значениям, ортогональны. Линейное преобразование конечномерного пространства Lявляется самосопряженным тогда и только тогда, когда в Lсуществует ортонормированный базис, состоящий из собственных векторов, и в этом базисе записывается действительной диагональной матрицей.

С. л. п. А наз. н е о т р и ц а т е л ь н ы м (или положительно полуопределенным), если 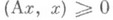для любого вектора х, и положительно определенным, если ( Ах, х)> 0 для любого вектора 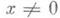. Для неотрицательности (положительной определенности) нек-рого С. л. п. в конечномерном пространстве необходимо и достаточно, чтобы все его собственные значения были неотрицательны (соответственно положительны) или чтобы соответствующая ему матрица была положительно полуопределенной (соответственно положительно определенной). В этом случае существует единственное неотрицательное С. л. п. В, удовлетворяющее условию В ²=А - квадратный корень из С. л. п. А.

А. Л. Онищик.