|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЯДЗначение РЯД в математической энциклопедии: , б е с к о н е ч н а я с у м м а,- последовательность элементов (наз. ч л е н а м и д а н н о г о р я д а) нек-рого линейного топологич. пространства и определенное бесконечное множество их конечных сумм (наз. ч а с т и ч н ы м и с у м м а м и р я да), для к-рых определено понятие предела. Простейшими примерами Р. являются следующие. Однократные числовые ряды. Пара последовательностей комплексных чисел { а п}и {sn} таких, что наз. ч и с л о в ы м (о д н о к р а т н ы м) р я д о м и обозначается так: или Элементы последовательности { а п}наз. ч л е н а м и р я д а, а элементы последовательности {sn} - его ч а с т и ч н ы м и с у м м а м и, причем а n наз. n-м членом Р. (2), a sn- его частичной суммой порядка п. Р. (2) однозначно определяется каждой из двух последовательностей { а п}и {sn}: члены последовательности {sn}получаются из членов последовательности { а n}по формуле (1), а последовательность { а n} восстанавливается по последовательности {sn} согласно формулам В этом смысле изучение Р. равносильно изучению последовательностей: для каждого утверждения о Р. можно сформулировать равносильное ему утверждение о последовательностях. Р. (2) наз. с х о д я щ и м с я, если последовательность его частичных сумм {sn} имеет конечный предел к-рый наз. с у м м о й Р. (2), и пишут Таким образом, обозначение (2) применяется как для самого Р., так и для его суммы. Если последовательность частичных сумм Р. (2) не имеет конечного предела, то он наз. р а с х о д я щ и м с я. Примером сходящегося Р. является сумма членов бесконечной геометрич. прогрессии Если Р. (2) сходится, то последовательность его членов стремится к нулю: Обратное утверждение неверно: последовательность членов стремится к нулю, однако этот Р. расходится. Ряд rn, то есть Если Р. (2) и ряд наз. с у м м о й рядов (2) и (3), причем его сумма равна сумме этих Р. Если Р. (2) сходится и l. - комплексное число, то ряд Условие сходимости Р., не использующее понятие его суммы, дает Коши критерий сходимости Р. Если все члены Р. (2) являются действительными числами: Для того чтобы Р. (5) сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Если же он расходится, то его частичные суммы стремятся к бесконечности: Для Р. с неотрицательными членами существует много различных признаков сходимости. Основными являются следующие. П р и з н а к с р а в н е н и я. Если для Р. (5) и с неотрицательными членами существует такая постоянная с > 0, что При применении признака сравнения для исследования сходимости заданного Р. с неотрицательными членами часто оказывается целесообразным выделить главную часть его n-го члена относительно виде сходящийся при a > 1 и расходящийся при Как следствие признака сравнения в случае, когда в качестве Р. сравнения взят Р. (7), получается следующее правило: если то при a > 1 и Следствиями признака сравнения являются также Д'Аламбера признак и Коши признак сходимости числовых рядов с положительными членами. Для таких Р. имеются еще Бертрана признак, Гаусса признак, Ермакова признак, Куммера признак, Раабе признак. Интегральный признак сходимости дает достаточные условия сходимости Р. (5) с неотрицательными членами, образующими убывающую последовательность: и где с - нек-рая постоянная, а Поэтому Р. (5) сходится тогда и только тогда, когда сходится интеграл . Если же Р. (5) расходится, то его частичные суммы sn растут так же, как интегралы т. е. sn асимптотически равны указанным интегралам: Для Р. (5), члены к-рого образуют убывающую последовательность, имеет место т е о р е м а К о ш и: если члены Р. (5) убывают, то он сходится или расходится одновременно с рядом Необходимым условием сходимости. Р. (5) с убывающей последовательностью членов является условие показывает, что условие (8) не является достаточным для сходимости Р. (5) с убывающей последовательностью членов. Важный класс числовых Р. составляют абсолютно сходящиеся ряды, т. е. такие Р. (2), для к-рых сходятся ряды Р. наз. у с л о в н о с х о д я щ и м и с я. Примером условно сходящегося Р. является ряд Сумма условно сходящегося Р. зависит от порядка его членов (см. Римана теорема о перестановке членов ряда): каковы бы ни были a и b принадлежащие множеству действительных чисел, дополненному бесконечностями Таким образом, для условно сходящихся Р. не имеет места коммутативный закон сложения. Не для всех Р. оказывается справедлив и ассоциативный закон сложения: если Р. расходится, то Р., полученный из данного последовательной группировкой его членов, может сходиться, причем его сумма зависит от способа группировки членов исходного Р. Напр., ряд расходится, а ряды (1-1)+(1-1)+. . . и 1-(1-1)- (1-1) -. . ., полученные из него попарной группировкой его членов, сходятся и имеют различные суммы. Однако если Р. сходится, то, конечно, всякий Р., получающийся последовательной группировкой его членов, сходится, и его суммой является сумма данного Р., ибо последовательность частичных сумм нового Р. есть подпоследовательность частичных сумм исходного Р. Среди Р. с членами разных знаков выделяют знакочередующиеся Р., для к-рых имеется Лейбница признак сходимости. Различные признаки сходимости для произвольных числовых Р. могут быть получены с помощью Абеля преобразования сумм попарных произведений, напр. Абеля признак, Дедекинда признак, Дирихле признак, Дюбуа-Реймона признак сходимости Р. У м н о ж е н и е р я д о в. Для умножения Р. существуют различные правила. Наиболее известно правило Коши, согласно к-рому при перемножении рядов (2) и (4) сначала суммируются по конечным "диагоналям" попарные произведения а тb п, т. е. такие, у к-рых сумма индексов т+п имеет одно и то же значение: и ряд Пусть Р. (2), (4), (9) сходятся и Если Р. (2) и (4) абсолютно сходятся, то Р. (9) также абсолютно сходится и аb=с. Если Р. (2) абсолютно сходится, а Р. (4) сходится, то сходится Р. (9) и ab=c (т е о р е м а М е р т е н с а). Если же ряды (2) и (4) условно сходятся, то Р. (9) может не сходиться; напр., ряд условно сходится, а ряд расходится. Если все три Р.-(2), (4), (9)-сходятся, то аb=с. Примером другого правила умножения Р. является суммирование сначала попарных произведений а тb п, у к-рых произведение индексов тп имеет фиксированное значение и определение произведения рядов (2) и (4) как ряда Встречаются также Р., члены к-рых an занумерованы всеми целыми числами и сумма этих Р. наз. суммой Р. (10). Числовыми Р. более сложной структуры являются кратные ряды, члены мультииндексами, где прямоугольные сферические и др. В зависимости от выбора типа частичных сумм определяется понятие суммы кратного Р. как соответствующего их предела. В случае m=2 кратный Р. наз. двойным рядом. Для кратных Р., в отличие от однократных, члены Р. уже могут не определяться заданием множества частичных сумм, т. е., вообще говоря, для того чтобы кратный Р. был определен, необходимо задать как кратную последовательность членов Р., так и множество его частичных сумм. В математич. анализе находят применение не только сходящиеся Р., но и расходящиеся. Для последних разработаны разнообразные методы суммирования. В виде сумм числовых Р. записываются многие важные иррациональные постоянные, напр.: а также значения определенных интегралов, первообразные подинтегральных функций к-рых не выражаются через элементарные функции: Функциональные ряды. ф ункциональным (о д н о к р а т н ы м) р я д о м наз. пара функциональных последовательностей { а п (х)}и {sn(x)}, состоящих из числовых функций, определенных на нек-ром множестве Xи таких, что Как и в случае числовых Р., элементы последовательности (a п (х)}наз. ч л е н а м и Р. (11), а последовательности {sn (х)} - его частичными суммами. Р. (11) наз. сходящимся на множестве X, если при любом фиксированном П р и м е р. Ряд сходится на всей комплексной плоскости, а ряд только при z=0. Сумма сходящегося Р. непрерывных, напр. на нек-ром отрезке, функций не обязательно является непрерывной функцией, напр. ряд сходится на отрезке [0, 1], его члены непрерывны на этом отрезке, а сумма разрывна в точке х=1. Ряд условий, при к-рых на функциональные Р. переносятся свойства непрерывности, дифференцируемости и интегрируемости конечных сумм соответственно непрерывных, дифференцируемых или интегрируемых функций, формулируется в терминах равномерной сходимости рядов (см. Равномерно сходящийся ряд). Р я д ы и з м е р и м ы х ф у н к ц и й. Пусть X - измеримое по Лебегу подмножество n-мерного евклидова пространства являются измеримыми почти всюду конечными на Xфункциями, принимающими значения из расширенной числовой прямой (т. е. наряду с действительными числами они могут принимать значения Пусть LP(X), при при Если Р. (12) сходится в Lp(X)и s(x)- его сумма, то существует подпоследовательность последовательности его частичных сумм, к-рая сходится к s(x)почти всюду на X. П о ч л е н н о е и н т е г р и р о в а н и е р я д о в. Обобщением теоремы о почленном интегрировании равномерно сходящихся Р. являются следующие теоремы. Т е о р е м а 1. Если существует такая суммируемая на множестве Xфункция f, что для всех m=1, 2,. . . и всех Р. (12) сходится почти всюду на Xи его сумма равна s(x), то Т е о р е м а 2. Если то имеет место формула (13). Можно почленно интегрировать и Р. (12), все члены к-рых неотрицательны на множестве X. У таких Р. последовательность их частичных сумм в каждой точке Т е о р е м а 3. Если члены Р. (12) неотрицательны, то имеет место формула (13). В предположениях теоремы 3 обе части формулы (13) могут обратиться в Т е о р е м а 4. Если члены Р. (12) неотрицательны и интегралы от его частичных сумм sm(x)ограничены в совокупности: где с-постоянная, то сумма s(х)Р. (12) является суммируемой функцией. П о ч л е н н о е д и ф ф е р е н ц и р о в а н и е р я д о в. Пусть и ряды Среди функциональных Р. особо важную роль играют степенные ряды, Фурье ряды, Дирихле ряды и вообще Р., получающиеся при разложении функций по собственным функциям того или иного оператора. Многие из перечисленных свойств функциональных Р. обобщаются на более общие Р., когда их членами являются функции со значениями в линейных нормированных пространствах или, более общо, в линейных топологич. пространствах, а также на кратные функциональные Р., то есть Р., члены к-рых снабжены мультииндексами: Теория функциональных рядов дает удобные и весьма общие методы для изучения функций, поскольку функции весьма широкого класса могут быть представлены в определенном смысле в виде суммы нек-рого ряда элементарных функций. Напр., однозначная аналитич. ция является в окрестности каждой внутренней точки из множества своего определения суммой своего Тейлора ряда;всякая непрерывная на отрезке функция является суммой равномерно сходящегося на этом отрезке ряда, членами к-рого являются алгебраич. многочлены; наконец, для всякой измеримой и конечной почти всюду на отрезке [-p, p] функции существует тригонометрич. ряд сумма к-рого почти всюду совпадает с заданной функцией. Разложение функций в Р. применяется в различных разделах математики: в анализе для исследования функций, при отыскании решений в виде Р. тех или иных уравнений, содержащих неизвестные функции, напр. неопределенных коэффициентов методом, в численных методах для приближенного вычисления значений функций и т. п. Историческая справка. К понятию бесконечных сумм подошли еще ученые Др. Греции, у них уже встречалась сумма членов бесконечной геометрич. прогрессии с положительным знаменателем, меньшим единицы. Как самостоятельное понятие Р. вошел в математику в 17 в. И. Ньютон (J. Newton) и Г. Лейбниц (G. Leibniz) систематически использовали Р. для решения как алгебраических, так и дифференциальных уравнений. Формальная теория Р. усиленно развивалась в 18- 19 вв. в работах Я. и И. Бернулли (Jakob und Johann Bernoulli), Б. Тейлора (В. Taylor), К. Маклорена (С. Maclaurin), Л. Эйлера (L. Euler), Ж. Д'Аламбера (J. D'Alembert), Ж. Лагранжа (J. Lagrange) и др. В этот период использовались как сходящиеся, так и расходящиеся Р., хотя не было полной ясности в вопросе о законности действий над ними. Точная теория Р. была создана в 19 в. на основе понятия предела в трудах К. Гаусса (С. Gauss), Б. Больцано (В. Bolzano), О. Коши (A. Cauchy), П. Дирихле (P. Dirichlet), Н. Абеля (N. Abel), К. Вейерштрасса (К. Weierstrass), В. Римана (В. Riemann) и др. Лит.:[1] К о л м о г о р о в А. Н., Ф о м и н С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [2] Л у з и н Н. Н., Теория функций действительного переменного, 2 изд., М., 1948; [3] Н и к о л ь с к и й С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977; [4] Х а р д и Г., Расходящиеся ряды, пер. с англ., М., 1951; [5] Б а х в а л о в Н. С., Численные методы, 2 изд., М., 1975; [6] И л ь и н В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971, 2 изд., ч. 2, М., 1980; [7] К у д р я в ц е в Л. Д., Курс математического анализа, т. 1-2, М., 1981; [8] Н и к о л ь с к и й С. М., Курс математического анализа, 2 изд., т. 1-2, М., 1975; [9] Н е м ы ц к и йВ., С л у д с к а я М., Ч е р к а с о в А., Курс математического анализа, 2 изд., т. 1-2, М.- Л., 1944. Л. Д. Кудрявцев. |
|
|
|

 (1)
(1)
 (2)
(2)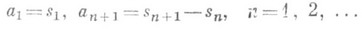


 (3) при условии, что
(3) при условии, что  . В этом случае ее сумма равна
. В этом случае ее сумма равна  , то есть
, то есть  . Если же
. Если же  , то Р. (3) дает пример расходящегося Р.
, то Р. (3) дает пример расходящегося Р.
 гармонического ряда
гармонического ряда
 наз. о с т а т к о м порядка пР. (2). Если Р. сходится, то каждый его остаток сходится. Если нек-рый остаток Р. сходится, то и сам Р. сходится. Если остаток порядка пР. (2) сходится и его сумма равна
наз. о с т а т к о м порядка пР. (2). Если Р. сходится, то каждый его остаток сходится. Если нек-рый остаток Р. сходится, то и сам Р. сходится. Если остаток порядка пР. (2) сходится и его сумма равна  , то
, то 
 (4) сходятся, то сходится и ряд
(4) сходятся, то сходится и ряд 
 , наз. п р о и з в е д е н и е м Р. (2) на число l, также сходится и
, наз. п р о и з в е д е н и е м Р. (2) на число l, также сходится и  .
. , то Р. (2) наз. действительным. Важную роль в теории Р. играют действительные Р. с неотрицательными членами:
, то Р. (2) наз. действительным. Важную роль в теории Р. играют действительные Р. с неотрицательными членами: (5)
(5) поэтому в этом случае пишут
поэтому в этом случае пишут 
 (6)
(6) то из сходимости Р. (6) следует сходимость Р. (5), а из расходимости Р. (5) - расходимость Р. (6).
то из сходимости Р. (6) следует сходимость Р. (5), а из расходимости Р. (5) - расходимость Р. (6). при
при  в
в  (а - нек-рая постоянная), а в качестве Р., с к-рым сравнивается данный Р., взять ряд
(а - нек-рая постоянная), а в качестве Р., с к-рым сравнивается данный Р., взять ряд  (7)
(7)

 Р. (5) сходится, а при
Р. (5) сходится, а при  и
и  Р. (5) расходится.
Р. (5) расходится. п= 1, 2,. . . Пусть Р. (5) таков, что для него существует функция f определенная и убывающая при
п= 1, 2,. . . Пусть Р. (5) таков, что для него существует функция f определенная и убывающая при  , у к-рой ее значения в целочисленных точках совпадают с членами данного ряда: f(n)=an, n=l, 2,. . . . Тогда если sn- частичные суммы, а rn - остатки ряда (5), то для них имеют место следующие оценки:
, у к-рой ее значения в целочисленных точках совпадают с членами данного ряда: f(n)=an, n=l, 2,. . . . Тогда если sn- частичные суммы, а rn - остатки ряда (5), то для них имеют место следующие оценки:


 .:
.:


 (8) Пример расходящегося ряда
(8) Пример расходящегося ряда 
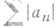 . Если Р. абсолютно сходится, то он просто сходится и его сумма не зависит от порядка следования слагаемых. Сходящиеся, но не абсолютно сходящиеся
. Если Р. абсолютно сходится, то он просто сходится и его сумма не зависит от порядка следования слагаемых. Сходящиеся, но не абсолютно сходящиеся 
 и
и  , можно так переставить члены любого условно сходящегося Р., членами к-рого являются действительные числа, что для частичных сумм sn полученного Р. будут иметь место равенства
, можно так переставить члены любого условно сходящегося Р., членами к-рого являются действительные числа, что для частичных сумм sn полученного Р. будут иметь место равенства 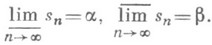

 (9)
(9) , членами к-рого являются полученные суммы, наз. п р о и з в е д е н и е м д а н н ы х Р. Это правило умножения Р. подсказывается формулой умножения степенных рядов:
, членами к-рого являются полученные суммы, наз. п р о и з в е д е н и е м д а н н ы х Р. Это правило умножения Р. подсказывается формулой умножения степенных рядов:

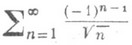


 . Это правило умножения Р. подсказывается формулой умножения Дирихле рядов:
. Это правило умножения Р. подсказывается формулой умножения Дирихле рядов:
 . Они обозначаются:
. Они обозначаются: (10) Р. (10) наз. с х о д я щ и м с я, если сходятся ряды
(10) Р. (10) наз. с х о д я щ и м с я, если сходятся ряды 
 к-рых снабжены
к-рых снабжены  - натуральные числа, k== 1, 2, . . ., т, т=2,3, .... В теории кратных Р. рассматриваются различные типы частичных сумм: треугольные
- натуральные числа, k== 1, 2, . . ., т, т=2,3, .... В теории кратных Р. рассматриваются различные типы частичных сумм: треугольные 
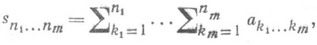



 (11)
(11)
 сходится числовой ряд
сходится числовой ряд 




 - мера Лебега и члены
- мера Лебега и члены  ряда
ряда  (12)
(12) и
и  ). Если Р. (12) сходится почти всюду на множестве X, то его сумма s(x)также является измеримой функцией и, в силу Егорова теоремы, для любого e > 0 существует такой компакт
). Если Р. (12) сходится почти всюду на множестве X, то его сумма s(x)также является измеримой функцией и, в силу Егорова теоремы, для любого e > 0 существует такой компакт 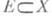 , что
, что  , а Р., членами к-рого являются сужения
, а Р., членами к-рого являются сужения  функций
функций  на компакте Е, сходится на нем равномерно и его суммой является
на компакте Е, сходится на нем равномерно и его суммой является 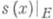 - сужение суммы Р. (12) на рассматриваемом компакте.
- сужение суммы Р. (12) на рассматриваемом компакте. ,- пространство функций
,- пространство функций  соответственно с нормой
соответственно с нормой 
 и с нормой
и с нормой 
 . P. (12) наз. с х о д я щ и м с я в пространстве Lp(X), если последовательность его частичных сумм {sn(x)}сходится в Lp(X)и ее предел s(x)наз. суммой Р. (12) в этом пространстве:
. P. (12) наз. с х о д я щ и м с я в пространстве Lp(X), если последовательность его частичных сумм {sn(x)}сходится в Lp(X)и ее предел s(x)наз. суммой Р. (12) в этом пространстве:
 частичные суммы sn(x)P. (12) удовлетворяют неравенству
частичные суммы sn(x)P. (12) удовлетворяют неравенству 
 (13)
(13)  ,
, 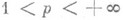 ,
,  , и последовательность частичных сумм {sm(x)}Р. (12) слабо сходится на множестве X к функции s(x)(т. <е. для любой функции
, и последовательность частичных сумм {sm(x)}Р. (12) слабо сходится на множестве X к функции s(x)(т. <е. для любой функции  , выполняется условие
, выполняется условие 
 возрастает и потому имеет конечный или бесконечный предел, к-рый наз. значением суммы s(x)рассматриваемого Р. в этой точке.
возрастает и потому имеет конечный или бесконечный предел, к-рый наз. значением суммы s(x)рассматриваемого Р. в этой точке. . Достаточные условия их конечности даются следующей теоремой.
. Достаточные условия их конечности даются следующей теоремой. , m = 1, 2, ...,
, m = 1, 2, ..., есть n-мерное арифметическое евклидово пространство точек х= (х 1, х2,. . ., х п),
есть n-мерное арифметическое евклидово пространство точек х= (х 1, х2,. . ., х п), , G - открытое в
, G - открытое в  множество,
множество,  . И пусть
. И пусть  - обобщенная производная функции f по переменной xi, i=l, 2,. . ., n. Если
- обобщенная производная функции f по переменной xi, i=l, 2,. . ., n. Если  ,
, (i0 - фиксировано),
(i0 - фиксировано),  ,
, , сходятся в
, сходятся в  ,то функция s(х)имеет в G обобщенную производную по переменной
,то функция s(х)имеет в G обобщенную производную по переменной  и
и  , то есть
, то есть 

