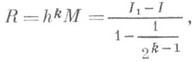" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

РУНГЕ ПРАВИЛО

Значение РУНГЕ ПРАВИЛО в математической энциклопедии:

- один пз методов оценки погрешности формул численного интегрирования. Пусть - остаточный член формулы численного интегрирования, где h - длина отрезка интегрирования или какой-то его части, k - фиксированное число и М - произведение постоянной на производную подинтегральной функции порядка k-1 в какой-то точке промежутка интегрирования. Если J - точное значение интеграла, а I - его приближенное значение, то

Согласно Р. п. вычисляется тот же самый интеграл по той же формуле численного интегрирования, но вместо hберется величина h/2. При этом, чтобы получить значение интеграла по всему отрезку, формула интегрирования применяется дважды. Если производная, входящая в М, меняется не сильно на рассматриваемом промежутке, то

где I₁ - значение интеграла, вычисленное по h/2. Р. п. используется и при численном решении дифференциальных уравнений. Правило предложено К. Рунге (С. Runge, нач. 20 в.).
Лит.:[1] Б е р е з и н И. С., Ж и д к о в Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2, М., 1962; [2] Современные численные методы решения обыкновенных дифференциальных уравнений, пер. с англ., М., 1979. А. Б. Иванов.