"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РИТЦА МЕТОД
Значение РИТЦА МЕТОД в математической энциклопедии:
- метод решения задач вариационного исчисления и вообще бесконечномерных задач на экстремум, основанный на минимизации функционала на конечномерных подпространствах или многообразиях.
Пусть поставлена задача нахождения точки минимума ограниченного снизу функционала  на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов
на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов 
 , полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1, . . .,jn, т. е. коэффициенты
, полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1, . . .,jn, т. е. коэффициенты  приближения
приближения

определяются из условия минимальности J ( и п )среди элементов указанного вида. Вместо координатной системы можно задать последовательность подпространств
 , не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением
, не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением  , А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения
, А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения  оператора Апо норме
оператора Апо норме  , порожденной скалярным произведением
, порожденной скалярным произведением 
 . Пусть нужно решить задачу
. Пусть нужно решить задачу
 (1)
(1)
Она равносильна задаче отыскания точки минимума квадратичного функционала

к-рый можно записать в виде
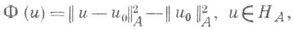
где и 0=А -1f- решение уравнения (1). Пусть  , n=1, 2, . . .,- замкнутые (обычно конечномерные) подпространства такие, что
, n=1, 2, . . .,- замкнутые (обычно конечномерные) подпространства такие, что  при
при  для каждого
для каждого  , где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и0 к решению уравнения (1); при этом
, где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и0 к решению уравнения (1); при этом 
при  . Если
. Если  - базис Н n, то коэффициенты элемента
- базис Н n, то коэффициенты элемента
 (2)
(2)
определяются из линейной системы уравнений
 (3)
(3)
К ритцовскому приближению можно прийти и минуя вариационную формулировку задачи (1). А именно, определив приближение (2) из условий

(м е т о д Г а л е р к и н а), приходят к той же системе уравнений (3). Поэтому Р. м. для уравнения (1) иногда наз. м е т о д о м Р и т ц а - Г а л е р к и н а.
Р. м. широко применяется и при решении задач на собственные значения, краевых задач и вообще операторных уравнений. Пусть Аи В - самосопряженные операторы в Н, причем А положительно определен, Вположителен,  и оператор А -1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А -1 В самосопряжен и положителен в HA и спектр задачи
и оператор А -1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А -1 В самосопряжен и положителен в HA и спектр задачи  (4) состоит из положительных собственных значений:
(4) состоит из положительных собственных значений:
 при
при 
Р. м. основан на вариационной характеризации собственных значений. Напр .,  и, проведя минимизацию лишь по подпространству
и, проведя минимизацию лишь по подпространству  , получают ритцовские приближения
, получают ритцовские приближения  к l1, и1. Если
к l1, и1. Если  , как и выше, базис Н п, то ритцовские приближения
, как и выше, базис Н п, то ритцовские приближения  к
к 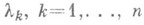 , определяются из уравнения
, определяются из уравнения

а вектор коэффициентов  приближения
приближения

к  определится как нетривиальное решение линейной однородной системы
определится как нетривиальное решение линейной однородной системы  . Р. м. приближает собственные значения сверху, то есть
. Р. м. приближает собственные значения сверху, то есть 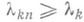 , k=l, . . ., п. Если k-е собственное значение задачи (4) простое
, k=l, . . ., п. Если k-е собственное значение задачи (4) простое  , то быстрота сходимости Р. м. характеризуется соотношениями
, то быстрота сходимости Р. м. характеризуется соотношениями

где  при
при  . Подобные соотношения распространяются и на случай кратного
. Подобные соотношения распространяются и на случай кратного  , но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.
, но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.
Лит.:[1] В а й н б е р г М. М., Вариационный метод и метод монотонных операторов в теории нелинейных уравнений, М., 1972; [2] К р а с н о с е л ь с к и й М. А. [и др.], Приближенное решение операторных уравнений, М., 1969; [3] М и х л и н С. Г., Вариационные методы в математической физике, 2 изд., М., 1970; [4] R i t z W., "J. reine und angew. Math.", 1908, Bd 135, S. 1-61. Г. М. Вайникко.

 на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов
на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов 
 , полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1, . . .,jn, т. е. коэффициенты
, полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1, . . .,jn, т. е. коэффициенты  приближения
приближения 
 , не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением
, не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением  , А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения
, А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения  оператора Апо норме
оператора Апо норме  , порожденной скалярным произведением
, порожденной скалярным произведением 
 . Пусть нужно решить задачу
. Пусть нужно решить задачу  (1)
(1)
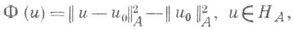
 , n=1, 2, . . .,- замкнутые (обычно конечномерные) подпространства такие, что
, n=1, 2, . . .,- замкнутые (обычно конечномерные) подпространства такие, что  при
при  для каждого
для каждого  , где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и0 к решению уравнения (1); при этом
, где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и0 к решению уравнения (1); при этом 
 . Если
. Если  - базис Н n, то коэффициенты элемента
- базис Н n, то коэффициенты элемента  (2)
(2) (3)
(3)
 и оператор А -1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А -1 В самосопряжен и положителен в HA и спектр задачи
и оператор А -1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А -1 В самосопряжен и положителен в HA и спектр задачи  (4) состоит из положительных собственных значений:
(4) состоит из положительных собственных значений: при
при 
 и, проведя минимизацию лишь по подпространству
и, проведя минимизацию лишь по подпространству  , получают ритцовские приближения
, получают ритцовские приближения  к l1, и1. Если
к l1, и1. Если  , как и выше, базис Н п, то ритцовские приближения
, как и выше, базис Н п, то ритцовские приближения  к
к 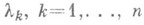 , определяются из уравнения
, определяются из уравнения 
 приближения
приближения 
 определится как нетривиальное решение линейной однородной системы
определится как нетривиальное решение линейной однородной системы  . Р. м. приближает собственные значения сверху, то есть
. Р. м. приближает собственные значения сверху, то есть 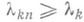 , k=l, . . ., п. Если k-е собственное значение задачи (4) простое
, k=l, . . ., п. Если k-е собственное значение задачи (4) простое  , то быстрота сходимости Р. м. характеризуется соотношениями
, то быстрота сходимости Р. м. характеризуется соотношениями 
 при
при  . Подобные соотношения распространяются и на случай кратного
. Подобные соотношения распространяются и на случай кратного  , но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.
, но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.