|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РИССА ТЕОРЕМА ВЫПУКЛОСТИЗначение РИССА ТЕОРЕМА ВЫПУКЛОСТИ в математической энциклопедии: логарифм In М(a, b) точной верхней грани модуля М(a, b) билинейной формы на множестве (если a=0 или b=0, то соответственно Обобщение Р. т. в. на линейные операторы (см. [3]): пусть Р. т. в. явилась отправным пунктом для целого направления в анализе, где изучаются интерполяционные свойства линейных операторов. Среди первых из обобщений Р. т. в.- т е о р е м а М а р ц и н к е в и ч а об интерполяции [5], к-рая гарантирует при Лит.:[1] R i е s z М., "Acta math.", 1926, v. 49, p. 465 - 97; [2] X а р д и Г., Л и т т л ь в у д Д., П о л и а Г., Неравенства, пер. с англ., М., 1948; [3] T h o r i n G., "Comm. Sem. Math. Univ. Lund.", 1939, v. 4, p. 1-5; [4] С т е й н И., В е й с Г., Введение н гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974; [5] М а r с i n k i e w i с z J., "С. r. Acad. Sci.", 1939, t. 208, p. 1272-73; [6] К р е й н С. Г., П е т у н и н Ю. И., С е м е н о в Е. М., Интерполяция линейных операторов, М., 1978; [7] Т r i e b e 1 Н., Interpolation theory, В., 1978. В. М. Тихомиров. |
|
|
|



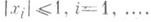 , тили
, тили  ) является выпуклой функцией от параметров a и b в области
) является выпуклой функцией от параметров a и b в области  , если форма действительна
, если форма действительна  , и в области
, и в области  , если форма комплексна
, если форма комплексна  . Эта теорема была доказана М. Риссом [1].
. Эта теорема была доказана М. Риссом [1]. ,- совокупность всех комплексозначных суммируемых в р-й степени при
,- совокупность всех комплексозначных суммируемых в р-й степени при  и существенно ограниченных при
и существенно ограниченных при  функций на нек-ром пространстве с мерой; пусть, далее,
функций на нек-ром пространстве с мерой; пусть, далее,
 ,- линейный непрерывный оператор; тогда Тявляется непрерывным оператором из
,- линейный непрерывный оператор; тогда Тявляется непрерывным оператором из  в
в  , где
, где  и норма kt оператора Т(как оператора из
и норма kt оператора Т(как оператора из  в
в  ) удовлетворяет неравенству
) удовлетворяет неравенству  (т. е. является логарифмически выпуклой функцией). Эту теорему наз. т е о р е м о й Р и с с а - Т о р и н а об интерполяции, но иногда т е о р е м о й в ы п у к л о с т и Р и с с а [4].
(т. е. является логарифмически выпуклой функцией). Эту теорему наз. т е о р е м о й Р и с с а - Т о р и н а об интерполяции, но иногда т е о р е м о й в ы п у к л о с т и Р и с с а [4].
 , непрерывность оператора
, непрерывность оператора 
 , при более слабых предположениях, чем в теореме Рисса - Торина. См. также Интерполирование операторов.
, при более слабых предположениях, чем в теореме Рисса - Торина. См. также Интерполирование операторов.