"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РИМАНОВО ПРОСТРАНСТВО ОБОБЩЕННОЕ
Значение РИМАНОВО ПРОСТРАНСТВО ОБОБЩЕННОЕ в математической энциклопедии:
- пространство с внутренней метрикой, подчиненное нек-рым ограничениям на кривизну. К ним относятся пространства с "кривизной, ограниченной сверху", и др. (см. [3]). Р. п. о. отличаются от римановых пространств не только большей общностью, но и тем, что они определяются и исследуются, исходя из метрики, без координат. При нек-ром соединении условий на кривизну и поведении кратчайших (т. е. кривых, длины к-рых равны расстояниям между концами) Р. п. о. оказывается римановым, что дает чисто метрич. определение риманова пространства.
Определения Р. п. о. исходят из классич. связи кривизны с избытком геодезического треугольника (избыток= сумма углов минус p). Эти понятия переносятся на пространство с внутренней метрикой такое, что у каждой точки его есть окрестность, любые две точки к-рой соединены кратчайшей. Это условие далее подразумевается без оговорок. Т р е у г о л ь н и к о м Т=АВС наз. тройка кратчайших АВ, ВС, СА - сторон треугольника, соединяющих попарно три различных точки А, В, С - вершины треугольника. Угол определяется между кривыми в любом метрич. пространстве.
Пусть L, M - исходящие из одной точки Окривые в пространстве с метрикой r. Выбираются точки  ,
,  , строится евклидов треугольник со сторонами х=r( О, X), у=r(O, Y), z=r(X, Y )и углом g( х, у), противолежащим стороне z. Определяется в е р х н и й у г о л между Lи М:
, строится евклидов треугольник со сторонами х=r( О, X), у=r(O, Y), z=r(X, Y )и углом g( х, у), противолежащим стороне z. Определяется в е р х н и й у г о л между Lи М:
 (1)
(1)
Верхние углы треугольника - это верхние углы  ,
,  между его сторонами при вершинах А, В, С, а избыток треугольника
между его сторонами при вершинах А, В, С, а избыток треугольника 
Р. п. о. с ограниченной кривизной 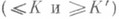 определяется условием:
определяется условием:
(А)для каждой последовательности треугольников Т n, стягивающихся к точке,
 (2)
(2)
где  - площадь евклидова треугольника с такими же сторонами, что
- площадь евклидова треугольника с такими же сторонами, что  , то
, то  Такое пространство оказывается римановым при двух естественных дополнительных условиях:
Такое пространство оказывается римановым при двух естественных дополнительных условиях:
(1) л о к а л ь н а я к о м п а к т н о с т ь п р о с тр а н с т в а (в пространстве с внутренней метрикой это уже обеспечивает условие локального существования кратчайших);
(2) л о к а л ь н а я п р о д о л ж а е м о с т ь к р а тч а й ш и х - у каждой точки существует окрестность Uтакая, что любую кратчайшую ХY, где  , можно продолжить за ее концы. При всех этих условиях пространство является римановым (см. [4]), причем в окрестности каждой точки можно ввести координаты х i так, что метрика будет задаваться линейным элементом
, можно продолжить за ее концы. При всех этих условиях пространство является римановым (см. [4]), причем в окрестности каждой точки можно ввести координаты х i так, что метрика будет задаваться линейным элементом  с коэффициентами
с коэффициентами  , 0<a<1. Тем самым имеется параллельный перенос (с непрерывными
, 0<a<1. Тем самым имеется параллельный перенос (с непрерывными  ) и почти везде - тензор кривизны.
) и почти везде - тензор кривизны.
Кроме того, доказано [7], что координаты х i можно взять гармоническими, т. е. удовлетворяющими равенствам  . Гармонич. системы координат составляют атлас класса С 3,a при любом a, 0<a<1.
. Гармонич. системы координат составляют атлас класса С 3,a при любом a, 0<a<1.
Р. п. о. с ограниченной кривизной при K = K', удовлетворяющее условиям (1) и (2), является римановым пространством постоянной римановой кривизны K(см. [3]).
Всякое риманово пространство с римановой кривизной, заключенной между Kи  , является Р. п. о. кривизны
, является Р. п. о. кривизны  и удовлетворяет условиям (1) и (2).
и удовлетворяет условиям (1) и (2).
"Пространство с кривизной  " определяется левым неравенством (2). т. е. условием:
" определяется левым неравенством (2). т. е. условием:
( А - )для любой последовательности треугольников Т п, стягивающихся в точку,
 (3)
(3)
Другое равносильное определение и начало исследования Р. п. о. исходят из сравнения произвольного треугольника Т=АВС с треугольником  со сторонами той же длины в пространстве постоянной кривизны K. Пусть
со сторонами той же длины в пространстве постоянной кривизны K. Пусть  - углы такого треугольника; относительный верхний избыток треугольника Топределяется как
- углы такого треугольника; относительный верхний избыток треугольника Топределяется как  . Условие ( А -) в определении пространства с кривизной
. Условие ( А -) в определении пространства с кривизной  можно заменить на условие:
можно заменить на условие:
(A1-). у каждой точки есть окрестность  , в к-рой
, в к-рой  для всякого треугольника Т. Выполняется и более сильное свойство вогнутости метрики. Именно, пусть L, М - кратчайшие, исходящие из одной точки О, и
для всякого треугольника Т. Выполняется и более сильное свойство вогнутости метрики. Именно, пусть L, М - кратчайшие, исходящие из одной точки О, и  - угол в треугольнике
- угол в треугольнике  со сторонами х=r(O, X), у=r(O, X), z=r(X, Y),
со сторонами х=r(O, X), у=r(O, X), z=r(X, Y), , в пространстве постоянной кривизны K, противолежащий стороне z. В
, в пространстве постоянной кривизны K, противолежащий стороне z. В  (локально) угол
(локально) угол  оказывается неубывающей функцией
оказывается неубывающей функцией  при
при 
 . Отсюда следуют локальные свойства:
. Отсюда следуют локальные свойства:
(I) между любыми двумя кратчайшими, исходящими из одной точки, существует угол и даже "угол в сильном смысле"  (так что, в частности, если
(так что, в частности, если
у=const, то  ;
;
(II) для углов a, b, g треугольника в  и соответствующего треугольника
и соответствующего треугольника 

(III) в  , если
, если  , кратчайшие
, кратчайшие  (тем самым кратчайшая в
(тем самым кратчайшая в  с данными концами единственна).
с данными концами единственна).
Двойственными пространствами с кривизной  будут пространства с кривизной
будут пространства с кривизной  , определяемые аналогично через нижние избытки, к-рые вычисляются по нижним углам в сильном смысле. Для кратчайших L, М этот угол есть
, определяемые аналогично через нижние избытки, к-рые вычисляются по нижним углам в сильном смысле. Для кратчайших L, М этот угол есть 
Нижний избыток треугольника есть  Пространство с кривизной
Пространство с кривизной  - это такое пространство, в к-ром вместо ( А - )выполняется условие:
- это такое пространство, в к-ром вместо ( А - )выполняется условие:
( А + )для любой последовательности Т n треугольников, стягивающихся к точке,
 (4)
(4)
Неравенство с верхним избытком  , противоположное неравенству (3), не дает содержательных результатов, их не дает и неравенство с избытком, вычисляемым просто с нижними углами
, противоположное неравенству (3), не дает содержательных результатов, их не дает и неравенство с избытком, вычисляемым просто с нижними углами

Условие ( А + )можно заменить на условие:
 , у каждой точки есть окрестность
, у каждой точки есть окрестность  , в к-рой
, в к-рой  для всякого треугольника Т. В
для всякого треугольника Т. В  (локально) угол
(локально) угол  для двух кратчайших L, M оказывается невозрастающей функцией (выпуклая метрика).
для двух кратчайших L, M оказывается невозрастающей функцией (выпуклая метрика).
Аналогично пространствам с кривизной  для пространств с кривизной
для пространств с кривизной  выполняются (локальные) свойства, подобные (I) и (II): между кратчайшими существует угол в сильном смысле;
выполняются (локальные) свойства, подобные (I) и (II): между кратчайшими существует угол в сильном смысле; 
 для всякого треугольника в
для всякого треугольника в  . Вместо (III) выполняется условие неналегания кратчайших или, что то же, единственность их продолжения: если АС Й АВ и АС1 Й АВ в
. Вместо (III) выполняется условие неналегания кратчайших или, что то же, единственность их продолжения: если АС Й АВ и АС1 Й АВ в  , то либо AC Й AC1, либо АС1 Й АС.
, то либо AC Й AC1, либо АС1 Й АС.
Таким образом, пространство с ограниченной кривизной получается соединением условий, определяющих оба класса пространств - с кривизной, ограниченной сверху или снизу (причем в левой части неравенства (3) нет нужды брать  ). Условие (А) можно заменить, подобно
). Условие (А) можно заменить, подобно  и
и  , на условие:
, на условие:
(A1) у каждой точки есть окрестность  ', где
', где  для всякого треугольника Т. Это оказывается также равносильным следующему:
для всякого треугольника Т. Это оказывается также равносильным следующему:
(А 2) для всякой четверки точек в  ' существует четверка точек с теми же попарными расстояниями в пространстве постоянной кривизны k, где
' существует четверка точек с теми же попарными расстояниями в пространстве постоянной кривизны k, где  и kзависит, вообще говоря, от выбранной четверки точек в
и kзависит, вообще говоря, от выбранной четверки точек в  '.
'.
Примером Р. п. о. с кривизной  является область риманова пространства, в к-рой римановы кривизны всех двумерных площадок во всех точках ограничены сверху (снизу) числом K(K').
является область риманова пространства, в к-рой римановы кривизны всех двумерных площадок во всех точках ограничены сверху (снизу) числом K(K').
Множество Vвпространстве с внутренней метрикой наз. в ы п у к л ы м, если любые две точки  можно соединить кратчайшей X, Y и всякая такая кратчайшая содержится в V.
можно соединить кратчайшей X, Y и всякая такая кратчайшая содержится в V.
Установлен [8] следующий результат: если пространство Rс внутренней метрикой получено склеиванием двух пространств R', R" кривизны  по выпуклым множествам V' М R" и V" М R", то Rсамо есть пространство кривизны
по выпуклым множествам V' М R" и V" М R", то Rсамо есть пространство кривизны  . Условие склеивания заключается в том, что
. Условие склеивания заключается в том, что  и в R', R" индуцируется метрика пространства R.
и в R', R" индуцируется метрика пространства R.
Две выходящие из точки Окривые L, М (по определению) имеют в О о д и н а к о в о е н а п р а в л е н и е, если верхний угол между ними равен нулю (если L=M, то говорят, что Lимеет в Оопределенное направление). Направление в точке Оопределяется как класс кривых, имеющих в Оодинаковое направление. Направления в точке Ообразуют метрич. пространство, в к-ром расстояние между направлениями определяется верхним углом между любыми их представителями. Это пространство наз. п р о с т р а нс т в о м н а п р а в л е н и й в точке О.
Доказано [5]: если точка Осодержится в окрестности пространства кривизны  , гомеоморфной Е n, то пространство направлений в точке Оявляется пространством кривизны
, гомеоморфной Е n, то пространство направлений в точке Оявляется пространством кривизны  . Неизвестно (1983), гомеоморфно ли оно (п-1)-мерной сфере.
. Неизвестно (1983), гомеоморфно ли оно (п-1)-мерной сфере.
В двумерном случае теория многообразий ограниченной кривизны (см. Двумерное многообразие ограниченной кривизны )включает в себя как частный случай теорию многообразий с кривизной  . Примером двумерного многообразия с кривизной
. Примером двумерного многообразия с кривизной  является линейчатая поверхность в
является линейчатая поверхность в  , снабженная внутренней метрикой, т. е. поверхность, образованная внутренними частями кратчайших, концы к-рых зачеркивают две спрямляемые кривые L1 L2. Если кривая L2 вырождается в точку О, поверхность наз. к о н у с о м к р а тч а й ш и х, натянутым из точки Она кривую L1. Если L1 есть треугольник ОАВ, то такой конус наз. поверхностным треугольником (см. [3]).
, снабженная внутренней метрикой, т. е. поверхность, образованная внутренними частями кратчайших, концы к-рых зачеркивают две спрямляемые кривые L1 L2. Если кривая L2 вырождается в точку О, поверхность наз. к о н у с о м к р а тч а й ш и х, натянутым из точки Она кривую L1. Если L1 есть треугольник ОАВ, то такой конус наз. поверхностным треугольником (см. [3]).
Отображение  метрич. пространства наз. н е р а с т я г и в а ю щ и м, если
метрич. пространства наз. н е р а с т я г и в а ю щ и м, если  , j(Y)) для любых
, j(Y)) для любых  . Отображение
. Отображение  замкнутой кривой Г 1 в М 1 на замкнутую кривую Г 2 в М 2 наз. э к в и л о н г а л ь н ы м, если длины соответствующих при отображении j дуг кривых Г 1 и Г 2 совпадают. Пусть V - выпуклая область в пространстве постоянной кривизны Kи L - краевой контур V. Область Vм а ж о р и р у е т замкнутую кривую Г в метрич. пространстве М, если существует нарастающее отображение области Vв М, эквилонгально отображающее Lна Г. Само отображение наз. м а ж о р и р у ющ и м.
замкнутой кривой Г 1 в М 1 на замкнутую кривую Г 2 в М 2 наз. э к в и л о н г а л ь н ы м, если длины соответствующих при отображении j дуг кривых Г 1 и Г 2 совпадают. Пусть V - выпуклая область в пространстве постоянной кривизны Kи L - краевой контур V. Область Vм а ж о р и р у е т замкнутую кривую Г в метрич. пространстве М, если существует нарастающее отображение области Vв М, эквилонгально отображающее Lна Г. Само отображение наз. м а ж о р и р у ющ и м.
Пусть  - выпуклое пространство с внутренней метрикой; С - конус кратчайших, натянутый на замкнутую спрямляемую кривую Г в
- выпуклое пространство с внутренней метрикой; С - конус кратчайших, натянутый на замкнутую спрямляемую кривую Г в  из точки
из точки  , причем в случае K>0 длина l кривой Г меньше
, причем в случае K>0 длина l кривой Г меньше  Тогда в пространстве постоянной кривизны Kсуществует выпуклая область V, мажорирующая Г, такая, что j(V)=C для соответствующего мажорирующего отображения j. Это свойство характеризует пространства кривизны
Тогда в пространстве постоянной кривизны Kсуществует выпуклая область V, мажорирующая Г, такая, что j(V)=C для соответствующего мажорирующего отображения j. Это свойство характеризует пространства кривизны  . Достаточным является уже существование эквилонгального нерастягивающего отображения контура Lобласти Vна Г.
. Достаточным является уже существование эквилонгального нерастягивающего отображения контура Lобласти Vна Г.
П о в е р х н о с т ь ю в метрич. пространстве Мназ. непрерывное отображение f круга Вв М. Пусть Р - триангулируемый многоугольник, т. е. комплекс из треугольников Т i, вписанный в В. Треугольнику Ti с вершинами X, Y, Z сопоставляется евклидов треугольник  со сторонами, равными расстоянию между точками f(X), f(Y), f(Z). Пусть S0(P)обозначает сумму площадей
со сторонами, равными расстоянию между точками f(X), f(Y), f(Z). Пусть S0(P)обозначает сумму площадей  всех треугольников
всех треугольников  ; тогда п л ощ а д ь S(f) п о в е р х н о с т и f определяется (см. [3]) как нижний предел величин S0(P)при условии, что вершины комплекса Рнеограниченно сгущаются в В: S(f)=lim S0(P). Это определение модифицировано так (см. [6]). Вместо точек f(X), f(Y), f(Z). вершинам X, Y, Z треугольника Т i комплекса Р сопоставляются нек-рые точки Х р, Yp, Zp в М, причем вершинам комплекса Рсопоставляются одинаковые точки в том и только в том случае, когда образы вершин при отображении f совпадают. За площадь L(f)поверхности f принимается нижний предел сумм площадей евклидовых треугольников
; тогда п л ощ а д ь S(f) п о в е р х н о с т и f определяется (см. [3]) как нижний предел величин S0(P)при условии, что вершины комплекса Рнеограниченно сгущаются в В: S(f)=lim S0(P). Это определение модифицировано так (см. [6]). Вместо точек f(X), f(Y), f(Z). вершинам X, Y, Z треугольника Т i комплекса Р сопоставляются нек-рые точки Х р, Yp, Zp в М, причем вершинам комплекса Рсопоставляются одинаковые точки в том и только в том случае, когда образы вершин при отображении f совпадают. За площадь L(f)поверхности f принимается нижний предел сумм площадей евклидовых треугольников  со сторонами, равными расстояниям между точками Х р, Yp, Zp при дополнительном предположении, что
со сторонами, равными расстояниям между точками Х р, Yp, Zp при дополнительном предположении, что  по всем вершинам
по всем вершинам  комплекса Рстремится к нулю. Всегда
комплекса Рстремится к нулю. Всегда 
1) Если последовательность поверхностей fn в RR, равномерно сходится к поверхности f, то
 (полунепрерывность).
(полунепрерывность).
2) Если р - нерастягивающее отображение из  в
в  и f - поверхность в
и f - поверхность в  , то
, то
 (принцип Колмогорова).
(принцип Колмогорова).
3) Площадь S(f) поверхностного треугольника Тв  не больше площади соответствующего треугольника
не больше площади соответствующего треугольника  и равна ему тогда и только тогда, когда треугольник Тизометричен
и равна ему тогда и только тогда, когда треугольник Тизометричен  (локальное свойство).
(локальное свойство).
4) В условиях теоремы о существовании мажорирующего отображения (см. выше) площадь S(G)не больше площади круга в пространстве постоянной кривизны Kс периметром l(изопериметрическое неравенство) (см. [3], [6]).
Решается [6] задача Плато в  о существовании поверхности минимальной площади, натянутой на замкнутую кривую Г. Доказано следующее. Пусть
о существовании поверхности минимальной площади, натянутой на замкнутую кривую Г. Доказано следующее. Пусть  - метрически полное пространство кривизны
- метрически полное пространство кривизны  (при K>0 диаметр
(при K>0 диаметр  , Г - замкнутая жорданова кривая в
, Г - замкнутая жорданова кривая в  . Тогда существует поверхность f минимальной площади L(f), натянутая на кривую Г. Пусть Г, Г n, n=1, 2, ... ,- замкнутые жордановы кривые в таком пространстве и а (Г), а (Г n) - минимальные площади поверхностей, натянутых соответственно на Г и Г n. Если Г n равномерно сходятся в нек-рых параметризациях к Г, то
. Тогда существует поверхность f минимальной площади L(f), натянутая на кривую Г. Пусть Г, Г n, n=1, 2, ... ,- замкнутые жордановы кривые в таком пространстве и а (Г), а (Г n) - минимальные площади поверхностей, натянутых соответственно на Г и Г n. Если Г n равномерно сходятся в нек-рых параметризациях к Г, то 
Рассматривались двумерные многообразия с индефинитной метрикой ограниченной кривизны. Не решена (1983) задача бескоординатного определения многомерных пространств с индефинитной метрикой ограниченной кривизны, в частности пространств общей теории относительности.
Лит.:[1] А л е к с а н д р о в А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948; [2] е г о ж е, "Труды Матем. ин-та АН СССР", 1951, т. 38, с. 5-23; [3] е г о ж е, "Schrift. Inst. Math. Deutsch. Acad. Wiss.", 1957, H. 1, S. 33- 84; [4] Б е р е с т о в с к и й В. Н., "Сиб. матем. ж.", 1975, т. 16, № 4, с. 651-62; [5] Н и к о л а е в И. Г., там же, 1978, т. 19, № 6, с. 1341-48; [6] е г о ж е, там же, 1979, т. 20, № 2,. с. 345-53; [7] Р е ш е т н я к Ю. Г., "Матем. сб.", 1960, т. 52, № 3, с. 789-98; [8] е г о ж е, "Сиб. матем. ж.", 1968, т. 9, № 4, с. 918-27. А. Д. Александров, В. Н. Берестовский.

 ,
,  , строится евклидов треугольник со сторонами х=r( О, X), у=r(O, Y), z=r(X, Y )и углом g( х, у), противолежащим стороне z. Определяется в е р х н и й у г о л между Lи М:
, строится евклидов треугольник со сторонами х=r( О, X), у=r(O, Y), z=r(X, Y )и углом g( х, у), противолежащим стороне z. Определяется в е р х н и й у г о л между Lи М: (1)
(1) ,
,  между его сторонами при вершинах А, В, С, а избыток треугольника
между его сторонами при вершинах А, В, С, а избыток треугольника 
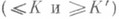 определяется условием:
определяется условием: (2)
(2) - площадь евклидова треугольника с такими же сторонами, что
- площадь евклидова треугольника с такими же сторонами, что  , то
, то  Такое пространство оказывается римановым при двух естественных дополнительных условиях:
Такое пространство оказывается римановым при двух естественных дополнительных условиях: , можно продолжить за ее концы. При всех этих условиях пространство является римановым (см. [4]), причем в окрестности каждой точки можно ввести координаты х i так, что метрика будет задаваться линейным элементом
, можно продолжить за ее концы. При всех этих условиях пространство является римановым (см. [4]), причем в окрестности каждой точки можно ввести координаты х i так, что метрика будет задаваться линейным элементом  с коэффициентами
с коэффициентами  , 0<a<1. Тем самым имеется параллельный перенос (с непрерывными
, 0<a<1. Тем самым имеется параллельный перенос (с непрерывными  ) и почти везде - тензор кривизны.
) и почти везде - тензор кривизны. . Гармонич. системы координат составляют атлас класса С 3,a при любом a, 0<a<1.
. Гармонич. системы координат составляют атлас класса С 3,a при любом a, 0<a<1. , является Р. п. о. кривизны
, является Р. п. о. кривизны  и удовлетворяет условиям (1) и (2).
и удовлетворяет условиям (1) и (2). " определяется левым неравенством (2). т. е. условием:
" определяется левым неравенством (2). т. е. условием: (3)
(3) со сторонами той же длины в пространстве постоянной кривизны K. Пусть
со сторонами той же длины в пространстве постоянной кривизны K. Пусть  - углы такого треугольника; относительный верхний избыток треугольника Топределяется как
- углы такого треугольника; относительный верхний избыток треугольника Топределяется как  . Условие ( А -) в определении пространства с кривизной
. Условие ( А -) в определении пространства с кривизной  можно заменить на условие:
можно заменить на условие: , в к-рой
, в к-рой  для всякого треугольника Т. Выполняется и более сильное свойство вогнутости метрики. Именно, пусть L, М - кратчайшие, исходящие из одной точки О, и
для всякого треугольника Т. Выполняется и более сильное свойство вогнутости метрики. Именно, пусть L, М - кратчайшие, исходящие из одной точки О, и  - угол в треугольнике
- угол в треугольнике  со сторонами х=r(O, X), у=r(O, X), z=r(X, Y),
со сторонами х=r(O, X), у=r(O, X), z=r(X, Y), , в пространстве постоянной кривизны K, противолежащий стороне z. В
, в пространстве постоянной кривизны K, противолежащий стороне z. В  (локально) угол
(локально) угол  оказывается неубывающей функцией
оказывается неубывающей функцией  при
при 
 . Отсюда следуют локальные свойства:
. Отсюда следуют локальные свойства: (так что, в частности, если
(так что, в частности, если  ;
; и соответствующего треугольника
и соответствующего треугольника 

 , если
, если  , кратчайшие
, кратчайшие  (тем самым кратчайшая в
(тем самым кратчайшая в  с данными концами единственна).
с данными концами единственна). будут пространства с кривизной
будут пространства с кривизной  , определяемые аналогично через нижние избытки, к-рые вычисляются по нижним углам в сильном смысле. Для кратчайших L, М этот угол есть
, определяемые аналогично через нижние избытки, к-рые вычисляются по нижним углам в сильном смысле. Для кратчайших L, М этот угол есть 
 Пространство с кривизной
Пространство с кривизной  - это такое пространство, в к-ром вместо ( А - )выполняется условие:
- это такое пространство, в к-ром вместо ( А - )выполняется условие: (4)
(4) , противоположное неравенству (3), не дает содержательных результатов, их не дает и неравенство с избытком, вычисляемым просто с нижними углами
, противоположное неравенству (3), не дает содержательных результатов, их не дает и неравенство с избытком, вычисляемым просто с нижними углами 
 , у каждой точки есть окрестность
, у каждой точки есть окрестность  , в к-рой
, в к-рой  для всякого треугольника Т. В
для всякого треугольника Т. В  (локально) угол
(локально) угол  для двух кратчайших L, M оказывается невозрастающей функцией (выпуклая метрика).
для двух кратчайших L, M оказывается невозрастающей функцией (выпуклая метрика). для пространств с кривизной
для пространств с кривизной  выполняются (локальные) свойства, подобные (I) и (II): между кратчайшими существует угол в сильном смысле;
выполняются (локальные) свойства, подобные (I) и (II): между кратчайшими существует угол в сильном смысле; 
 для всякого треугольника в
для всякого треугольника в  . Вместо (III) выполняется условие неналегания кратчайших или, что то же, единственность их продолжения: если АС Й АВ и АС1 Й АВ в
. Вместо (III) выполняется условие неналегания кратчайших или, что то же, единственность их продолжения: если АС Й АВ и АС1 Й АВ в  , то либо AC Й AC1, либо АС1 Й АС.
, то либо AC Й AC1, либо АС1 Й АС. ). Условие (А) можно заменить, подобно
). Условие (А) можно заменить, подобно  и
и  , на условие:
, на условие: ', где
', где  для всякого треугольника Т. Это оказывается также равносильным следующему:
для всякого треугольника Т. Это оказывается также равносильным следующему: ' существует четверка точек с теми же попарными расстояниями в пространстве постоянной кривизны k, где
' существует четверка точек с теми же попарными расстояниями в пространстве постоянной кривизны k, где  и kзависит, вообще говоря, от выбранной четверки точек в
и kзависит, вообще говоря, от выбранной четверки точек в  '.
'. является область риманова пространства, в к-рой римановы кривизны всех двумерных площадок во всех точках ограничены сверху (снизу) числом K(K').
является область риманова пространства, в к-рой римановы кривизны всех двумерных площадок во всех точках ограничены сверху (снизу) числом K(K'). можно соединить кратчайшей X, Y и всякая такая кратчайшая содержится в V.
можно соединить кратчайшей X, Y и всякая такая кратчайшая содержится в V. по выпуклым множествам V' М R" и V" М R", то Rсамо есть пространство кривизны
по выпуклым множествам V' М R" и V" М R", то Rсамо есть пространство кривизны  . Условие склеивания заключается в том, что
. Условие склеивания заключается в том, что  и в R', R" индуцируется метрика пространства R.
и в R', R" индуцируется метрика пространства R. , гомеоморфной Е n, то пространство направлений в точке Оявляется пространством кривизны
, гомеоморфной Е n, то пространство направлений в точке Оявляется пространством кривизны  . Неизвестно (1983), гомеоморфно ли оно (п-1)-мерной сфере.
. Неизвестно (1983), гомеоморфно ли оно (п-1)-мерной сфере. . Примером двумерного многообразия с кривизной
. Примером двумерного многообразия с кривизной  является линейчатая поверхность в
является линейчатая поверхность в  , снабженная внутренней метрикой, т. е. поверхность, образованная внутренними частями кратчайших, концы к-рых зачеркивают две спрямляемые кривые L1 L2. Если кривая L2 вырождается в точку О, поверхность наз. к о н у с о м к р а тч а й ш и х, натянутым из точки Она кривую L1. Если L1 есть треугольник ОАВ, то такой конус наз. поверхностным треугольником (см. [3]).
, снабженная внутренней метрикой, т. е. поверхность, образованная внутренними частями кратчайших, концы к-рых зачеркивают две спрямляемые кривые L1 L2. Если кривая L2 вырождается в точку О, поверхность наз. к о н у с о м к р а тч а й ш и х, натянутым из точки Она кривую L1. Если L1 есть треугольник ОАВ, то такой конус наз. поверхностным треугольником (см. [3]). метрич. пространства наз. н е р а с т я г и в а ю щ и м, если
метрич. пространства наз. н е р а с т я г и в а ю щ и м, если  , j(Y)) для любых
, j(Y)) для любых  . Отображение
. Отображение  замкнутой кривой Г 1 в М 1 на замкнутую кривую Г 2 в М 2 наз. э к в и л о н г а л ь н ы м, если длины соответствующих при отображении j дуг кривых Г 1 и Г 2 совпадают. Пусть V - выпуклая область в пространстве постоянной кривизны Kи L - краевой контур V. Область Vм а ж о р и р у е т замкнутую кривую Г в метрич. пространстве М, если существует нарастающее отображение области Vв М, эквилонгально отображающее Lна Г. Само отображение наз. м а ж о р и р у ющ и м.
замкнутой кривой Г 1 в М 1 на замкнутую кривую Г 2 в М 2 наз. э к в и л о н г а л ь н ы м, если длины соответствующих при отображении j дуг кривых Г 1 и Г 2 совпадают. Пусть V - выпуклая область в пространстве постоянной кривизны Kи L - краевой контур V. Область Vм а ж о р и р у е т замкнутую кривую Г в метрич. пространстве М, если существует нарастающее отображение области Vв М, эквилонгально отображающее Lна Г. Само отображение наз. м а ж о р и р у ющ и м. - выпуклое пространство с внутренней метрикой; С - конус кратчайших, натянутый на замкнутую спрямляемую кривую Г в
- выпуклое пространство с внутренней метрикой; С - конус кратчайших, натянутый на замкнутую спрямляемую кривую Г в  из точки
из точки  , причем в случае K>0 длина l кривой Г меньше
, причем в случае K>0 длина l кривой Г меньше  Тогда в пространстве постоянной кривизны Kсуществует выпуклая область V, мажорирующая Г, такая, что j(V)=C для соответствующего мажорирующего отображения j. Это свойство характеризует пространства кривизны
Тогда в пространстве постоянной кривизны Kсуществует выпуклая область V, мажорирующая Г, такая, что j(V)=C для соответствующего мажорирующего отображения j. Это свойство характеризует пространства кривизны  . Достаточным является уже существование эквилонгального нерастягивающего отображения контура Lобласти Vна Г.
. Достаточным является уже существование эквилонгального нерастягивающего отображения контура Lобласти Vна Г. со сторонами, равными расстоянию между точками f(X), f(Y), f(Z). Пусть S0(P)обозначает сумму площадей
со сторонами, равными расстоянию между точками f(X), f(Y), f(Z). Пусть S0(P)обозначает сумму площадей  всех треугольников
всех треугольников  ; тогда п л ощ а д ь S(f) п о в е р х н о с т и f определяется (см. [3]) как нижний предел величин S0(P)при условии, что вершины комплекса Рнеограниченно сгущаются в В: S(f)=lim S0(P). Это определение модифицировано так (см. [6]). Вместо точек f(X), f(Y), f(Z). вершинам X, Y, Z треугольника Т i комплекса Р сопоставляются нек-рые точки Х р, Yp, Zp в М, причем вершинам комплекса Рсопоставляются одинаковые точки в том и только в том случае, когда образы вершин при отображении f совпадают. За площадь L(f)поверхности f принимается нижний предел сумм площадей евклидовых треугольников
; тогда п л ощ а д ь S(f) п о в е р х н о с т и f определяется (см. [3]) как нижний предел величин S0(P)при условии, что вершины комплекса Рнеограниченно сгущаются в В: S(f)=lim S0(P). Это определение модифицировано так (см. [6]). Вместо точек f(X), f(Y), f(Z). вершинам X, Y, Z треугольника Т i комплекса Р сопоставляются нек-рые точки Х р, Yp, Zp в М, причем вершинам комплекса Рсопоставляются одинаковые точки в том и только в том случае, когда образы вершин при отображении f совпадают. За площадь L(f)поверхности f принимается нижний предел сумм площадей евклидовых треугольников  со сторонами, равными расстояниям между точками Х р, Yp, Zp при дополнительном предположении, что
со сторонами, равными расстояниям между точками Х р, Yp, Zp при дополнительном предположении, что  по всем вершинам
по всем вершинам  комплекса Рстремится к нулю. Всегда
комплекса Рстремится к нулю. Всегда 
 (полунепрерывность).
(полунепрерывность). в
в  и f - поверхность в
и f - поверхность в  , то
, то  (принцип Колмогорова).
(принцип Колмогорова). не больше площади соответствующего треугольника
не больше площади соответствующего треугольника  и равна ему тогда и только тогда, когда треугольник Тизометричен
и равна ему тогда и только тогда, когда треугольник Тизометричен  (локальное свойство).
(локальное свойство). о существовании поверхности минимальной площади, натянутой на замкнутую кривую Г. Доказано следующее. Пусть
о существовании поверхности минимальной площади, натянутой на замкнутую кривую Г. Доказано следующее. Пусть  - метрически полное пространство кривизны
- метрически полное пространство кривизны  (при K>0 диаметр
(при K>0 диаметр  , Г - замкнутая жорданова кривая в
, Г - замкнутая жорданова кривая в  . Тогда существует поверхность f минимальной площади L(f), натянутая на кривую Г. Пусть Г, Г n, n=1, 2, ... ,- замкнутые жордановы кривые в таком пространстве и а (Г), а (Г n) - минимальные площади поверхностей, натянутых соответственно на Г и Г n. Если Г n равномерно сходятся в нек-рых параметризациях к Г, то
. Тогда существует поверхность f минимальной площади L(f), натянутая на кривую Г. Пусть Г, Г n, n=1, 2, ... ,- замкнутые жордановы кривые в таком пространстве и а (Г), а (Г n) - минимальные площади поверхностей, натянутых соответственно на Г и Г n. Если Г n равномерно сходятся в нек-рых параметризациях к Г, то 