|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕЗначение РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ в математической энциклопедии: -линейное однородное обыкновенное дифференциальное уравнение 2-го порядка в комплексной плоскости, имеющее три заданные регулярные особые точки а, b, с с соответствующими характеристич. показателями a. a', b, b', g, g' в этих точках. Общий вид такого уравнения впервые выписал Э. Паппериц (Е. Papperitz), из-за чего оно также наз. Папперица уравнением. Решения Р. д. у. записываются в виде так наз. Р- фу н к ц и и Р и м а н а Р. д. у. принадлежит Фукса классу уравнений с тремя особыми точками. Частным случаем Р. д. у. является гипергеометрическое уравнение (особые точки: Лит. см. при ст. Папперица уравнение. Н. X. Розов. |
|
|
|
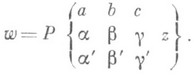
); поэтому само Р. д. у. иногда наз. о б о б щ е н н ы м г и п е р г е о м е т р и ч е с к и м у р а в н е н и е м. Р. д. у. приводится к Похгаммера уравнению, а потому решение Р. д. у. можно записать в виде интеграла по специальному контуру в комплексной плоскости.