Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕКУРРЕНТНОЕ СООТНОШЕНИЕЗначение РЕКУРРЕНТНОЕ СООТНОШЕНИЕ в математической энциклопедии: рекуррентная формула,- соотношение вида к-рое позволяет вычислять все члены последовательности а 1, а 2, а 3,. . ., если заданы ее первые рчленов. Примеры Р. с.: 1) В случае, когда Р. с. линейно (см. Возвратная последовательность), задача описания множества всех последовательностей, удовлетворяющих данному Р. с., имеет аналогии с решением обыкновенного однородного линейного дифференциального уравнения с постоянными коэффициентами. Лит.:[1] М а р к у ш е в и ч А. И., Возвратные последовательности, 2 изд., М., 1975. С. Н. Артемов. |
|
|
|

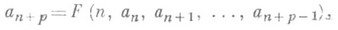
 - геометрич. прогрессия, 2) an +1=an+d - арифметич. прогрессия, 3) а n+ 2= = а n+1+ а n -последовательность чисел Фибоначчи.
- геометрич. прогрессия, 2) an +1=an+d - арифметич. прогрессия, 3) а n+ 2= = а n+1+ а n -последовательность чисел Фибоначчи.