"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕДУКТИВНОЕ ПРОСТРАНСТВО
Значение РЕДУКТИВНОЕ ПРОСТРАНСТВО в математической энциклопедии:
такое однородное пространство G/Hсвязной группы Ли G, что в алгебре Ли  группы G существует
группы G существует  (H)-инвариантное подпространство, дополнительное к подалгебре
(H)-инвариантное подпространство, дополнительное к подалгебре  , являющейся алгеброй Ли группы H. Выполнение любого из следующих условий достаточно для того, чтобы однородное пространство G/Hбыло Р. п.: 1) линейная группа
, являющейся алгеброй Ли группы H. Выполнение любого из следующих условий достаточно для того, чтобы однородное пространство G/Hбыло Р. п.: 1) линейная группа  (Н)вполне приводима, 2) на
(Н)вполне приводима, 2) на  существует
существует  (H)-инвариантная билинейная форма, сужение к-рой на
(H)-инвариантная билинейная форма, сужение к-рой на  невырождено. В частности, всякое однородное риманово пространство является Р. п. Если M=G/H- Р. п. и группа G действует эффективно на М, то линейное представление изотропии группы Нв касательном пространстве М 0 к многообразию Мв точке
невырождено. В частности, всякое однородное риманово пространство является Р. п. Если M=G/H- Р. п. и группа G действует эффективно на М, то линейное представление изотропии группы Нв касательном пространстве М 0 к многообразию Мв точке  точно. С каждым
точно. С каждым  инвариантным подпространством
инвариантным подпространством  , дополнительным к
, дополнительным к  , связаны две важные G-инвариантные аффинные связности на М:. к а н о н и ч е с к а я с в я зн о с т ь и е с т е с т в е н н а я с в я з н о с т ь б е з к р у ч е н и я. Канонич. связность на Р. п. M=G/H с фиксированным
, связаны две важные G-инвариантные аффинные связности на М:. к а н о н и ч е с к а я с в я зн о с т ь и е с т е с т в е н н а я с в я з н о с т ь б е з к р у ч е н и я. Канонич. связность на Р. п. M=G/H с фиксированным  -инвариантным разложением
-инвариантным разложением  - единственная G-инвариантная аффинная связность на М, обладающая тем свойством, что для любого вектора
- единственная G-инвариантная аффинная связность на М, обладающая тем свойством, что для любого вектора  и любого репера ив точке o кривая (exp tX)uв главном расслоении реперов над Мгоризонтальна. Канонич. связность полна и множество се геодезических, проходящих через точку о, совпадает с множеством кривых вида (exp tX) о, где
и любого репера ив точке o кривая (exp tX)uв главном расслоении реперов над Мгоризонтальна. Канонич. связность полна и множество се геодезических, проходящих через точку о, совпадает с множеством кривых вида (exp tX) о, где  После естественного отождествления пространств
После естественного отождествления пространств  и М 0 тензор кривизны Rи тензор кручения Тканонич. связности определяются формулами
и М 0 тензор кривизны Rи тензор кручения Тканонич. связности определяются формулами 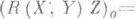
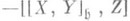 и
и  , где X, Y,
, где X, Y,  , а через
, а через  и
и  обозначены проекции вектора
обозначены проекции вектора  на
на  и
и  соответственно. Тензорные поля Rи Тпараллельны относительно канонич. связности так же, как и любое другое G-инвариантное тензорное поле на М. Алгебра Ли линейной группы голономии (см. Голономии группа).канонич. связности на Mс опорной точкой опорождается множеством
соответственно. Тензорные поля Rи Тпараллельны относительно канонич. связности так же, как и любое другое G-инвариантное тензорное поле на М. Алгебра Ли линейной группы голономии (см. Голономии группа).канонич. связности на Mс опорной точкой опорождается множеством 
 , где l - линейное представление изотропии алгебры Ли
, где l - линейное представление изотропии алгебры Ли  в пространстве М 0. Всякое связное односвязное многообразие, снабженное полной аффинной связностью с параллельными полями кривизны и кручения, может быть представлено в виде Р. п., канонич. связность к-рого совпадает с заданной аффинной связностью. На Р. п. M=G/Hс фиксированным
в пространстве М 0. Всякое связное односвязное многообразие, снабженное полной аффинной связностью с параллельными полями кривизны и кручения, может быть представлено в виде Р. п., канонич. связность к-рого совпадает с заданной аффинной связностью. На Р. п. M=G/Hс фиксированным  -инвариантным разложением
-инвариантным разложением  существует единственная G-инвариантная аффинная связность с нулевым кручением, имеющая те же геодезические, что и канонич. связность. Эта связность наз. естественной с в я з н о с т ь ю б е з к р у ч ен и я на М(относительно разложения
существует единственная G-инвариантная аффинная связность с нулевым кручением, имеющая те же геодезические, что и канонич. связность. Эта связность наз. естественной с в я з н о с т ь ю б е з к р у ч ен и я на М(относительно разложения  ). Однородное риманово или псевдориманово пространство M=G/Hназ. е с т е с т в е н н о р е д у к т и в н ы м, если оно допускает такое
). Однородное риманово или псевдориманово пространство M=G/Hназ. е с т е с т в е н н о р е д у к т и в н ы м, если оно допускает такое  -инвариантное разложение
-инвариантное разложение  , что
, что
 (*)
(*)
для всех  , где В - невырожденная симметрическая билинейная форма на m, индуцированная римановой (псевдоримановой) структурой на Мпри естественном отождествлении пространств
, где В - невырожденная симметрическая билинейная форма на m, индуцированная римановой (псевдоримановой) структурой на Мпри естественном отождествлении пространств  и
и  . Если M=G/H- естественно редуктивное риманово или псевдориманово пространство с фиксированным
. Если M=G/H- естественно редуктивное риманово или псевдориманово пространство с фиксированным  инвариантным разложением
инвариантным разложением 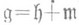 , удовлетворяющим условию (*), то естественная связность без кручения совпадает с соответствующей римановой или псевдоримановой связностью на М. Если М - одно-связное естественно редуктивное однородное риманово пространство и
, удовлетворяющим условию (*), то естественная связность без кручения совпадает с соответствующей римановой или псевдоримановой связностью на М. Если М - одно-связное естественно редуктивное однородное риманово пространство и 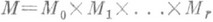 - его разложение де Рама, то Мможет быть представлено в виде
- его разложение де Рама, то Мможет быть представлено в виде  , причем
, причем 
 и
и 
Важным обобщением Р. п. являются v-редуктивные однородные пространства [4]. Однородное пространство  наз.
наз.  -р е д у к т и в н ы м, если его стационарная подалгебра
-р е д у к т и в н ы м, если его стационарная подалгебра 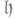 допускает разложение в прямую сумму подпространств
допускает разложение в прямую сумму подпространств  , где
, где  , причем в
, причем в  существует такое дополнительное к
существует такое дополнительное к  подпространство
подпространство  , что
, что 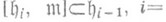
 , где
, где  . При этом 1-редуктивные однородные пространства - это в точности Р. п.; примерами 2-редуктивных однородных пространств являются проективное и конформное пространства, на к-рых действуют группа проективных преобразований и группа конформных преобразований соответственно. Если
. При этом 1-редуктивные однородные пространства - это в точности Р. п.; примерами 2-редуктивных однородных пространств являются проективное и конформное пространства, на к-рых действуют группа проективных преобразований и группа конформных преобразований соответственно. Если  есть
есть  -редуктивное однородное пространство и
-редуктивное однородное пространство и  , то линейное представление изотропии алгебры Ли
, то линейное представление изотропии алгебры Ли  не является точным (так как
не является точным (так как  при i>l) и, следовательно, на Мне существует G-инвариантной аффинной связности. Однако на
при i>l) и, следовательно, на Мне существует G-инвариантной аффинной связности. Однако на 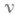 -ре-дуктивном однородном пространстве существует каноническая G-инвариантная связность, слоем к-рой является однородное пространство нек-рой транзитивно-дифференциальной группы порядка
-ре-дуктивном однородном пространстве существует каноническая G-инвариантная связность, слоем к-рой является однородное пространство нек-рой транзитивно-дифференциальной группы порядка  (см. [4]).
(см. [4]).
Наряду с Р. п. рассматриваются также ч а с т и ч н о р е д у к т и в н ы е п р о с т р а н с т в а, т. е. такие однородные пространства  , что существует разложение алгебры Ли
, что существует разложение алгебры Ли  в прямую сумму двух ненулевых
в прямую сумму двух ненулевых  -инвариантных подпространств, одно из к-рых содержит подалгебру
-инвариантных подпространств, одно из к-рых содержит подалгебру  (см. [5]).
(см. [5]).
Лит.:[1] К о б а я с и Ш., Н о м и д з у К., Основы дифференциальной геометрии, пер. с англ., т. 2, М., 1981; [2] Ра ш е в с к и й П. К., "Тр. Семинара по вект. и тенз. анализу", 1952, в. 9, с. 49-74; [3] N о m i z u K., "Amer. J. Math.", 1954, v. 76, № 1, p. 33-65; [4] К а н т о р И. Л., "Тр. Семинара по вект. и тенз. анализу", 1966, в. 13, с. 310-98; [5] В и н б е р г Э. Б., "Тр. Моск. матем. об-ва", 1960, т. 9, с. 191-210.
Д. В, Алексеевский.

 группы G существует
группы G существует  (H)-инвариантное подпространство, дополнительное к подалгебре
(H)-инвариантное подпространство, дополнительное к подалгебре  , являющейся алгеброй Ли группы H. Выполнение любого из следующих условий достаточно для того, чтобы однородное пространство G/Hбыло Р. п.: 1) линейная группа
, являющейся алгеброй Ли группы H. Выполнение любого из следующих условий достаточно для того, чтобы однородное пространство G/Hбыло Р. п.: 1) линейная группа  (Н)вполне приводима, 2) на
(Н)вполне приводима, 2) на  существует
существует  (H)-инвариантная билинейная форма, сужение к-рой на
(H)-инвариантная билинейная форма, сужение к-рой на  невырождено. В частности, всякое однородное риманово пространство является Р. п. Если M=G/H- Р. п. и группа G действует эффективно на М, то линейное представление изотропии группы Нв касательном пространстве М 0 к многообразию Мв точке
невырождено. В частности, всякое однородное риманово пространство является Р. п. Если M=G/H- Р. п. и группа G действует эффективно на М, то линейное представление изотропии группы Нв касательном пространстве М 0 к многообразию Мв точке  точно. С каждым
точно. С каждым  инвариантным подпространством
инвариантным подпространством  , дополнительным к
, дополнительным к  , связаны две важные G-инвариантные аффинные связности на М:. к а н о н и ч е с к а я с в я зн о с т ь и е с т е с т в е н н а я с в я з н о с т ь б е з к р у ч е н и я. Канонич. связность на Р. п. M=G/H с фиксированным
, связаны две важные G-инвариантные аффинные связности на М:. к а н о н и ч е с к а я с в я зн о с т ь и е с т е с т в е н н а я с в я з н о с т ь б е з к р у ч е н и я. Канонич. связность на Р. п. M=G/H с фиксированным  -инвариантным разложением
-инвариантным разложением  - единственная G-инвариантная аффинная связность на М, обладающая тем свойством, что для любого вектора
- единственная G-инвариантная аффинная связность на М, обладающая тем свойством, что для любого вектора  и любого репера ив точке o кривая (exp tX)uв главном расслоении реперов над Мгоризонтальна. Канонич. связность полна и множество се геодезических, проходящих через точку о, совпадает с множеством кривых вида (exp tX) о, где
и любого репера ив точке o кривая (exp tX)uв главном расслоении реперов над Мгоризонтальна. Канонич. связность полна и множество се геодезических, проходящих через точку о, совпадает с множеством кривых вида (exp tX) о, где  После естественного отождествления пространств
После естественного отождествления пространств  и М 0 тензор кривизны Rи тензор кручения Тканонич. связности определяются формулами
и М 0 тензор кривизны Rи тензор кручения Тканонич. связности определяются формулами 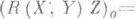
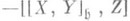 и
и  , где X, Y,
, где X, Y,  , а через
, а через  и
и  обозначены проекции вектора
обозначены проекции вектора  на
на  и
и  соответственно. Тензорные поля Rи Тпараллельны относительно канонич. связности так же, как и любое другое G-инвариантное тензорное поле на М. Алгебра Ли линейной группы голономии (см. Голономии группа).канонич. связности на Mс опорной точкой опорождается множеством
соответственно. Тензорные поля Rи Тпараллельны относительно канонич. связности так же, как и любое другое G-инвариантное тензорное поле на М. Алгебра Ли линейной группы голономии (см. Голономии группа).канонич. связности на Mс опорной точкой опорождается множеством 
 , где l - линейное представление изотропии алгебры Ли
, где l - линейное представление изотропии алгебры Ли  в пространстве М 0. Всякое связное односвязное многообразие, снабженное полной аффинной связностью с параллельными полями кривизны и кручения, может быть представлено в виде Р. п., канонич. связность к-рого совпадает с заданной аффинной связностью. На Р. п. M=G/Hс фиксированным
в пространстве М 0. Всякое связное односвязное многообразие, снабженное полной аффинной связностью с параллельными полями кривизны и кручения, может быть представлено в виде Р. п., канонич. связность к-рого совпадает с заданной аффинной связностью. На Р. п. M=G/Hс фиксированным  -инвариантным разложением
-инвариантным разложением  существует единственная G-инвариантная аффинная связность с нулевым кручением, имеющая те же геодезические, что и канонич. связность. Эта связность наз. естественной с в я з н о с т ь ю б е з к р у ч ен и я на М(относительно разложения
существует единственная G-инвариантная аффинная связность с нулевым кручением, имеющая те же геодезические, что и канонич. связность. Эта связность наз. естественной с в я з н о с т ь ю б е з к р у ч ен и я на М(относительно разложения  ). Однородное риманово или псевдориманово пространство M=G/Hназ. е с т е с т в е н н о р е д у к т и в н ы м, если оно допускает такое
). Однородное риманово или псевдориманово пространство M=G/Hназ. е с т е с т в е н н о р е д у к т и в н ы м, если оно допускает такое  -инвариантное разложение
-инвариантное разложение  , что
, что  (*)
(*) , где В - невырожденная симметрическая билинейная форма на m, индуцированная римановой (псевдоримановой) структурой на Мпри естественном отождествлении пространств
, где В - невырожденная симметрическая билинейная форма на m, индуцированная римановой (псевдоримановой) структурой на Мпри естественном отождествлении пространств  и
и  . Если M=G/H- естественно редуктивное риманово или псевдориманово пространство с фиксированным
. Если M=G/H- естественно редуктивное риманово или псевдориманово пространство с фиксированным  инвариантным разложением
инвариантным разложением 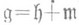 , удовлетворяющим условию (*), то естественная связность без кручения совпадает с соответствующей римановой или псевдоримановой связностью на М. Если М - одно-связное естественно редуктивное однородное риманово пространство и
, удовлетворяющим условию (*), то естественная связность без кручения совпадает с соответствующей римановой или псевдоримановой связностью на М. Если М - одно-связное естественно редуктивное однородное риманово пространство и 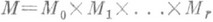 - его разложение де Рама, то Мможет быть представлено в виде
- его разложение де Рама, то Мможет быть представлено в виде  , причем
, причем 
 и
и 
 наз.
наз.  -р е д у к т и в н ы м, если его стационарная подалгебра
-р е д у к т и в н ы м, если его стационарная подалгебра 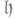 допускает разложение в прямую сумму подпространств
допускает разложение в прямую сумму подпространств  , где
, где  , причем в
, причем в  существует такое дополнительное к
существует такое дополнительное к  подпространство
подпространство  , что
, что 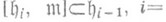
 , где
, где  . При этом 1-редуктивные однородные пространства - это в точности Р. п.; примерами 2-редуктивных однородных пространств являются проективное и конформное пространства, на к-рых действуют группа проективных преобразований и группа конформных преобразований соответственно. Если
. При этом 1-редуктивные однородные пространства - это в точности Р. п.; примерами 2-редуктивных однородных пространств являются проективное и конформное пространства, на к-рых действуют группа проективных преобразований и группа конформных преобразований соответственно. Если  есть
есть  -редуктивное однородное пространство и
-редуктивное однородное пространство и  , то линейное представление изотропии алгебры Ли
, то линейное представление изотропии алгебры Ли  не является точным (так как
не является точным (так как  при i>l) и, следовательно, на Мне существует G-инвариантной аффинной связности. Однако на
при i>l) и, следовательно, на Мне существует G-инвариантной аффинной связности. Однако на 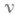 -ре-дуктивном однородном пространстве существует каноническая G-инвариантная связность, слоем к-рой является однородное пространство нек-рой транзитивно-дифференциальной группы порядка
-ре-дуктивном однородном пространстве существует каноническая G-инвариантная связность, слоем к-рой является однородное пространство нек-рой транзитивно-дифференциальной группы порядка  (см. [4]).
(см. [4]). , что существует разложение алгебры Ли
, что существует разложение алгебры Ли  в прямую сумму двух ненулевых
в прямую сумму двух ненулевых  -инвариантных подпространств, одно из к-рых содержит подалгебру
-инвариантных подпространств, одно из к-рых содержит подалгебру  (см. [5]).
(см. [5]).