|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГУЛЯРНОСТИ ПРИЗНАКИЗначение РЕГУЛЯРНОСТИ ПРИЗНАКИ в математической энциклопедии: д л я м е т о д о в с у м м и р о в а н и я - условия регулярности суммирования метода. Для матричного метода суммирования, определенного преобразованием последовательности в последовательность посредством матрицы являются необходимыми и достаточными для регулярности метода суммирования. Для матричного метода суммирования, определенного преобразованием ряда в последовательность посредством матрицы Условия (1) первоначально были установлены О. Тёплицем [1] для треугольных методов суммирования, а затем X. Штейнхаузом [2] распространены на произвольные матричные методы суммирования. В связи с этим матрицу, удовлетворяющую условиям (1), наз. м а т р и ц е й Т ё п л и ц а, или Т-м а т р и ц е й. Для полунепрерывных методов суммирования, определенных преобразованием последовательности в функцию посредством полунепрерывной матрицы Регулярный матричный метод суммирования является в п о л н е р е г у л я р н ы м, если все элементы матрицы преобразования неотрицательны. Это условие в общем случае не является необходимым для полной регулярности. Лит.:[1] Т o e p l i t z О., "Prace mat.-fizyczne", 1911, v. 22, p. 113-19; [2] S t е i n h a u s Н., там же, р. 121 - 34; [3] X a p д и Г., Расходящиеся ряды, пер. с англ., М., 1951; [4] К у к Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960. И. И. Волков. |
|
|
|

 условия:
условия:  (1)
(1)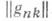 , n, k=1,2, . . ., необходимыми и достаточными условиями регулярности являются:
, n, k=1,2, . . ., необходимыми и достаточными условиями регулярности являются: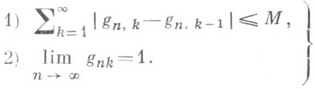 (2)
(2) или преобразованием ряда в функцию посредством полунепрерывной матрицы
или преобразованием ряда в функцию посредством полунепрерывной матрицы  , Р. п. подобны соответственно условиям (1) и (2).
, Р. п. подобны соответственно условиям (1) и (2).